高斯消元

ACM

高斯消元的主要方法有：

  • 化为上三角矩阵再回代求解；
  • 用gauss_jordan法化为对角矩阵后求解；

二进制高斯消元只用到了符号^(亦或),消元的方法和上面的完全一样。只不过运算符号由原来的加减乘除变成了只有(^)亦或。

高斯消元

大家应该都学过线性代数，那么就不讲高斯消元的原理了。下面着重介绍高斯消元算法的步骤:

化成上三角矩阵的高斯消元

  • 假设正在处理第i行，那么要找到一行使得\( \left|a_{ri}\right| \)大于\( \left|a_{ii}\right| \)，然后交换这两行，后面的i+1~n行与第i行进行消元。
  • 变成上三角矩阵后再回代。

适用的范围：要求原来的系数矩阵可逆。
消元的顺序:

上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <bits/stdc++.h>
using namespace std;
const int maxn = 110;
//要求系数矩阵是可逆的
//这里的A是增广矩阵，A[~][n]是伴随矩阵，最后的结果也是保存在伴随矩阵中的
//矩阵的规模为n*(n+1)
void Guass_elimination(double A[][maxn], int n){
    for(int i=0; i<n; i++){
        int r = i;
        for(int j=i+1; j<n; j++){
            if(fabs(A[j][i])>fabs(A[i][i])) r = j;
        }
        //将绝对值最大的换到主行的位置
        if(r!=i)
            for(int j=0; j<=n; j++) swap(A[i][j], A[r][j]);
        //第i+1~n行根据第i行进行消元
        for(int k=i+1; k<n; k++){
            double f = A[k][i] / A[i][i];//为了让那一列除主行外所有的元素为0，要乘的系数
            for(int j=i; j<=n; j++){
                A[k][j] -= f*A[i][j];
            }
        }
    }
    //回代
    for(int i=n-1; i>=0; i--){
        for(int j=i+1; j<n; j++){
            A[i][n] -= A[j][n]*A[i][j];
        }
        A[i][n] /= A[i][i];
    }
}
int main()
{
    /*测试矩阵
    {{1, 1/2, 0, 1},
     {1, -1, 0, 0},
     {0, 1/2, -1, 0}
    }
    答案是{2, 2, 1}
    */
    double A[maxn][maxn];
    A[0][0] = 1, A[0][1] = -0.5, A[0][2] = 0, A[0][3] = 1;
    A[1][0] = 1, A[1][1] = -1, A[1][2] = 0, A[1][3] = 0;
    A[2][0] = 0, A[2][1] = 0.5, A[2][2] = -1, A[2][3] = 0;
    Guass_elimination(A, 3);
    for(int i=0; i<3; i++){
        printf("%lf\n", A[i][3]);
    }
    return 0;
}

更高精度的消元

精度的缺失是中间的一步：

1
double f = A[k][i] / A[i][i];

保存了一个要乘的系数，从而过早的进行了消元。为了满足高精度的要求，我们在最后一时刻前都保存这A[k][i].从而消元的过程要逆着
总之不用中间的变量来保存系数，这样会减少精度的误差
消元的顺序:

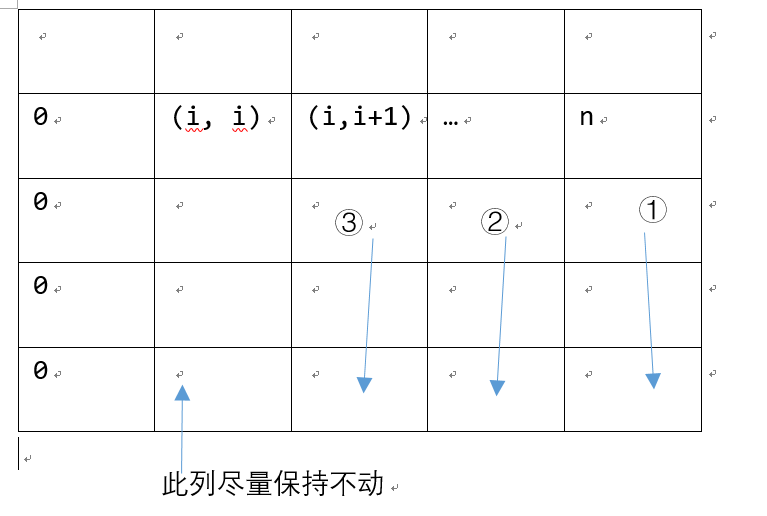
1
2
3
4
for(int j=n; j>=i; j--){
    for(int k=i+1; k<n; k++)
        A[k][j] -= A[k][i]/A[i][i]*A[i][j];
}

下面是高精度的化成上三角高斯消元的板子：
应用的条件：原来的系数矩阵必须可逆！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <bits/stdc++.h>
using namespace std;
const int maxn = 110;
void Guass_elimination(double A[][maxn], int n){
    for(int i=0; i<n; i++){
        int r = i;
        for(int j=i+1; j<n; j++){
            if(fabs(A[j][i])>fabs(A[i][i])) r = j;
        }
        //将绝对值最大的换到主行的位置
        if(r!=i)
            for(int j=0; j<=n; j++) swap(A[i][j], A[r][j]);
        //第i+1~n行根据第i行进行消元
        for(int j=n; j>=i; j--){
            for(int k=i+1; k<n; k++)
                A[k][j] -= A[k][i]/A[i][i]*A[i][j];
        }
    }
    //回代
    for(int i=n-1; i>=0; i--){
        for(int j=i+1; j<n; j++){
            A[i][n] -= A[j][n]*A[i][j];
        }
        A[i][n] /= A[i][i];
    }
}

化成对角矩阵的Guass_jordan算法：

应用的范围：

  • 可以判断是否有解，有无数的解，还是无解。
  • 省略了上面的回代过程。
  • 运算量比之前的上三角矩阵要大。

题目

10828 - Back to Kernighan-Ritchie

题意

DAG图，一个程序从编号为1的节点进入，问每个节点执行程序的期望的次数。

题解

设第i个节点的期望的次数为\(x_i\),它的出度为\(d[x_i]\), 设它有前驱节点\(x_{s_1}, x_{s_2}, \cdots, x_{s_n}\).
那么
$$ \sum_{j=s1}^{sn} \frac{x_j}{d[x_j]} = x_i\ $$

其中由于一开始程序从编号为1的节点进入，那么计算\(x_1\)时上式的左边还有加上1.

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include<algorithm>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
const double eps = 1e-8;
const int maxn = 100 + 10;
typedef double Matrix[maxn][maxn];
// 由于本题的特殊性，消元后不一定是对角阵，甚至不一定是阶梯阵
// 但若x[i]解惟一且有限，第i行除了A[i][i]和A[i][n]之外的其他元素均为0
void gauss_jordan(Matrix A, int n) {
  int i, j, k, r;
  for(i = 0; i < n; i++) {
    r = i;
    for(j = i+1; j < n; j++)
      if (fabs(A[j][i]) > fabs(A[r][i])) r = j;
    if(fabs(A[r][i]) < eps) continue; // 放弃这一行，直接处理下一行 (*)
    if(r != i) for(j = 0; j <= n; j++) swap(A[r][j], A[i][j]);
    // 与除了第i行外的其他行进行消元
    for(k = 0; k < n; k++) if(k != i)
      for(j = n; j >= i; j--) A[k][j] -= A[k][i]/A[i][i] * A[i][j];
  }
}
Matrix A;
int n, d[maxn];
vector<int> prev[maxn];
int inf[maxn];
int main() {
  int kase = 0;
  while(scanf("%d", &n) == 1 && n) {
    memset(d, 0, sizeof(d));
    for(int i = 0; i < n; i++) prev[i].clear();
    int a, b;
    while(scanf("%d%d", &a, &b) == 2 && a) {
      a--; b--; // 改成从0开始编号
      d[a]++; // 结点a的出度加1
      prev[b].push_back(a);
    }
    // 构造方程组
    memset(A, 0, sizeof(A));
    for(int i = 0; i < n; i++) {
      A[i][i] = 1;
      for(int j = 0; j < prev[i].size(); j++)
        A[i][prev[i][j]] -= 1.0 / d[prev[i][j]];
      if(i == 0) A[i][n] = 1;
    }
    // 解方程组，标记无穷变量
    gauss_jordan(A, n);
    memset(inf, 0, sizeof(inf));
    for(int i = n-1; i >= 0; i--) {
      if(fabs(A[i][i])<eps && fabs(A[i][n])>eps) inf[i] = 1; // 直接解出来的无穷变量
      for(int j = i+1; j < n; j++)
        if(fabs(A[i][j])>eps && inf[j]) inf[i] = 1; // 和无穷变量扯上关系的变量也是无穷的
    }
    int q, u;
    scanf("%d", &q);
    printf("Case #%d:\n", ++kase);
    while(q--) {
      scanf("%d", &u); u--;
      if(inf[u]) printf("infinity\n");
      else printf("%.3lf\n", fabs(A[u][u])<eps ? 0.0 : A[u][n]/A[u][u]);
    }
  }
  return 0;
}

进一步的说明

若是下面的情况：

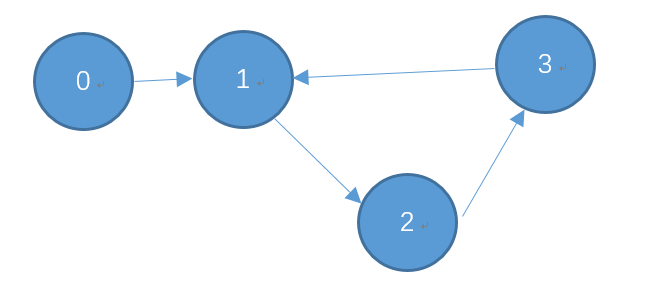
可以列出下面的矩阵：
$$
\left(
\begin{array}{ccc|c}
1 & 0 & -1 & 1\\
1 & -1 & 0 & 0\\
0 & 1 & -1 & 0\\
\end{array}
\right)
\Rightarrow
\left(
\begin{array}{ccc|c}
1 & 0 & -1 & 1\\
0 & -1 & 1 & -1\\
0 & 0 & 0 & -1\\
\end{array}
\right)
$$

在我们的认知中，出现上面的式子是无解的情况，但是实际的情况它是有无数解的。
书上留下了一个结论：

  • 当A[i][i] = A[i][n] = 0时， \(x_i\) = 0；
  • 当A[i][i] = 0但A[i][n]>0时，\(x_i\)为正无穷(上面的例子A[i][n]不一定保证为正吧)。我还不是很清楚其中的原因(待解决)，不过当我们无法判断的时候不妨带入到具体的例子中来解释，例如上面我画的例子。

二进制高斯消元

二进制高斯消元主要解决的是一类开关问题，最重要的是能够理解其中的含义：
规定：

  • 一个格子只有0、1两种状态。
  • 将一个格子按下之后，这个格子本身和上下左右的格子都变成相反的状态。

那么我们讨论一下为什么可以使用亦或(^)来描述这种状态的转变:

  • 若一个格子原来的状态是0，我们按下它旁边的一个格子，那么(0^1)=1,满足我们想要的表达的状态；若旁边的一个格子又按下(1^1)=0,依旧满足。
  • 若一个格子的原来状态是1，那么按下它旁边的一个格子，那么(1^1)=0,依次类推。
    总结：亦或运算有一种很好的状态转换的性质，还比如在treap中左孩子右旋，右孩子左旋的应用。（还记得吗QaQ?）
    关于亦或(^)的很多其他有趣的性质，请自行百度！！

下面用具体的题目来说明

题目

EXTENDED LIGHTS OUT

题意

给了5*6的格子，初始状态给定：0表示灯初始为灭的状态， 1表示灯初始为亮的状态。要求按下一些按钮之后，所有的灯都变成灭(0).

题解

本题由于规模比较的小，可以使用枚举法。先枚举行的状态。
但是在这个专题里面我们使用二进制高斯消元。
首先对原来的格子进行编号：

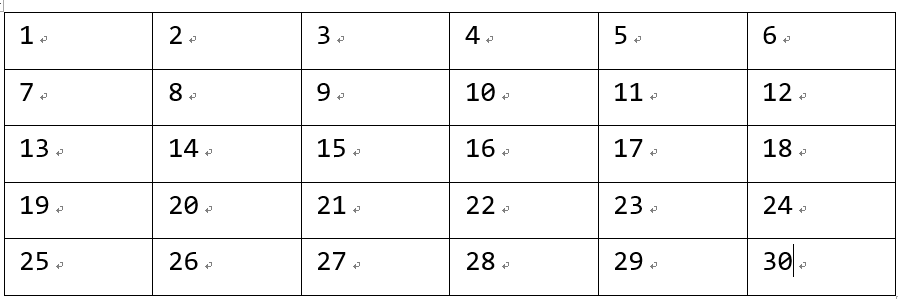
$$\begin{cases}
a_{11} \bigotimes a_{12} \bigotimes a_{21} \bigotimes state_1= 0 \\
a_{12} \bigotimes a_{11} \bigotimes a_{13} \bigotimes a_{22} \bigotimes state_2 = 0 \\
\cdots \\
a_{21} \bigotimes a_{22} \bigotimes a_{11} \bigotimes a_{31} \bigotimes state_7 = 0\\
a_{21} \bigotimes a_{22} \bigotimes a_{23} \bigotimes a_{12} \bigotimes a_{32} \bigotimes state_8 = 0\\
\cdots \\
a_{55} \bigotimes a_{56} \bigotimes a_{46} \bigotimes state_{30} = 0
\end{cases}
$$
两边同时对\(state_i\)进行亦或，变一下型：

$$\begin{cases}
a_{11} \bigotimes a_{12} \bigotimes a_{21} = state_1 \\
a_{12} \bigotimes a_{11} \bigotimes a_{13} \bigotimes a_{22} = state_2 \\
\cdots \\
a_{21} \bigotimes a_{22} \bigotimes a_{11} \bigotimes a_{31} = state_7\\
a_{21} \bigotimes a_{22} \bigotimes a_{23} \bigotimes a_{12} \bigotimes a_{32} = state_8\\
\cdots \\
a_{55} \bigotimes a_{56} \bigotimes a_{46} = state_{30}
\end{cases}
$$
说明:\( state_i \)表示第i个格子的初始的状态
在一个方程中，若旁边的格子按下对一个\(state_i\)有影响，那么将所有的对i这个格子的影响亦或起来,最后的状态是灭(0).

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
const int d[5][2] = {{0, 0}, {0, 1}, {0, -1}, {1, 0}, {-1, 0}};
int t, a[31][31], out[6][6];
void back()
{
    for (int i = 29; i >= 0; i--)
        out[i / 6][i % 6] = a[i][30];
}
void guess()
{
    for(int i=0; i<30; i++){
        int k=i;
        for(; k<30; k++){
            if(a[k][i])break;
        }
        for(int j=i; j<=30; j++){
            swap(a[i][j], a[k][j]);
        }
        for(int j=0; j<30; j++){
            if(j == i) continue;
            if(a[j][i]){
                for(int s=i; s<=30; s++){
                    a[j][s]^=a[i][s];
                }
            }
        }
    }
    back();
}
int main()
{
    int cas = 0;
    scanf("%d", &t);
    while (t--)
    {
        memset(a, 0, sizeof(a));
        for (int i = 0; i < 30; i++)
            scanf("%d", &a[i][30]);
        for (int i = 0; i < 30; i++)
        {
            int x = i / 6, y = i % 6;
            for (int j = 0; j < 5; j++)
            {
                int xx = x + d[j][0];
                int yy = y + d[j][1];
                if (xx < 0 || xx >= 5 || yy < 0 || yy >= 6) continue;
                a[i][xx * 6 + yy] = 1;
            }
        }
        guess();
        printf("PUZZLE #%d\n", ++cas);
        for (int i = 0; i < 5; i++)
        {
            for (int j = 0; j < 5; j++)
                printf("%d ", out[i][j]);
            printf("%d\n", out[i][5]);
        }
    }
    return 0;
}

未解决的问题

如何超高精度的计算值呢？听数一说过好像有一种不断相减不断缩小系数的方法不会产生浮点数，类似于gcd的求解一样。

本文标题:高斯消元

文章作者:Babydragon

发布时间:2017-10-04, 11:16:24

最后更新:2018-03-23, 13:36:05

原始链接:http://baolintian.github.io/2017/10/04/高斯消元/

许可协议: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

文章目录
  1. 1. 高斯消元
    1. 1.1. 化成上三角矩阵的高斯消元
      1. 1.1.1. 更高精度的消元
    2. 1.2. 化成对角矩阵的Guass_jordan算法：
      1. 1.2.1. 应用的范围：
      2. 1.2.2. 题目
      3. 1.2.3. 题意
      4. 1.2.4. 题解
      5. 1.2.5. AC代码
    3. 1.3. 进一步的说明
  2. 2. 二进制高斯消元
    1. 2.1. 题目
    2. 2.2. 题意
    3. 2.3. 题解
    4. 2.4. AC代码
  3. 3. 未解决的问题
{{ live2d() }}