一般图的匹配

ACM

这个算法理解起来比较的困难，而且网上很多博客讲的不够具体，甚至有些是错误的。这次我将用一个例子来演示这个算法的流程，帮助理解。
不涉及证明：它的算法思路和匈牙利算法相似，只不过多出来了一个处理奇环的操作。

题目

一般图的最大匹配

题解

一般图的最大匹配裸题

一般图最大匹配的算法流程

思路流程引用自带花树算法初学
规定三类点：

  • id[i] = -1 :表示节点i从未访问过
  • id[i] = 0 :表示这个点是可拓展点（S点，不妨理解为start,相当于新的寻找点）
  • id[i] = 1: 表示这个点是待寻找新的匹配点的点（T点，不妨理解为terminal点）
    举例说明：一个图是 1—2—3,(2,3)之前匹配好了，现在轮到1节点去找增广路，id[1] = 0。遇到2号节点是匹配好的，id[2] = 1, id[3] = 0.相当于将1转移到了3节点，再从3号节点去寻找增广路径。

流程：

  1. 从未匹配过的点x出发寻找增广路，假设找到了y,并且id[y] = -1,有下面的两种情况：
    ①y没有匹配边，那么结束算法，(x, y)匹配成功。
    ②y有匹配边，那么使id[y] = 1, 假设y的匹配节点为z，使id[z] = 0。

  2. id[y] = 0.此时说明遇到了奇环。且x, y在这个环中距离他们的lca是最远的。我们试图将(x, y)之间连一条匹配边，如果环中有一个点可以连接外面的点。

  3. id[y] = 1.跳过对这个点的探索。

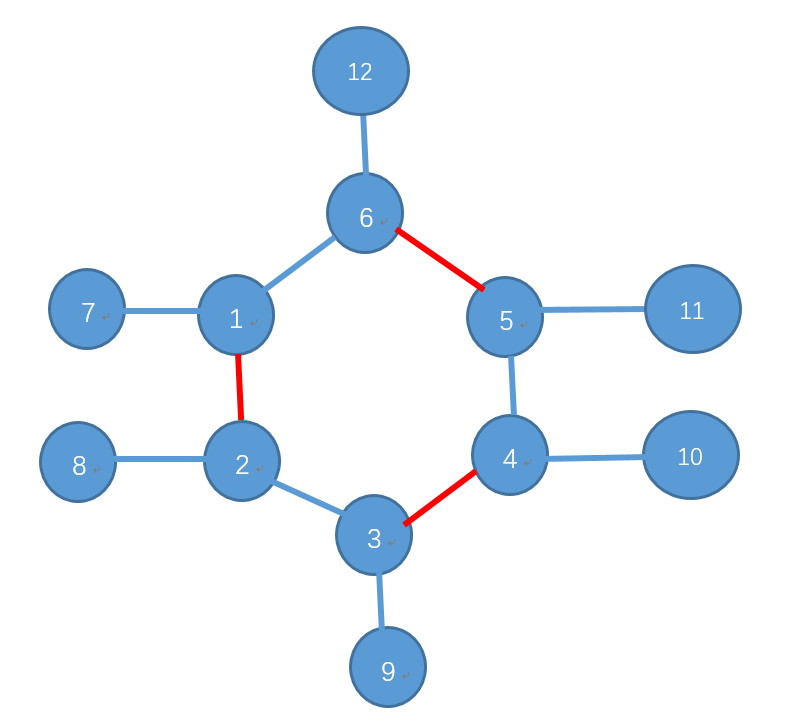
奇环的例子

样例：
6 6
1 5 1 2 2 3 3 4 4 6 4 5
因为是用链式前向星来存图的，所以图的顺序是逆过来的。

初始状态：



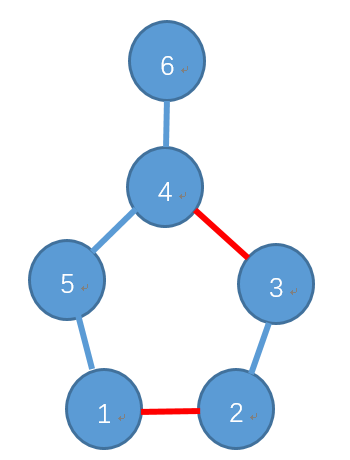
一开始的匹配：



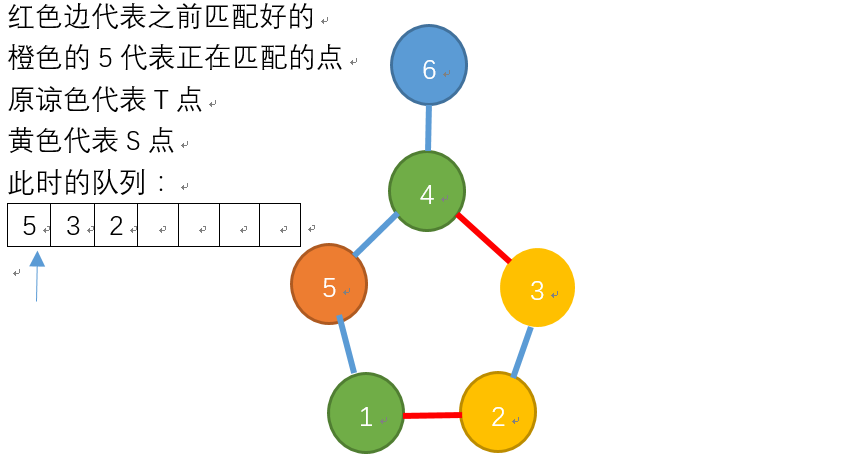
待匹配的5号节点，以及入队的点：



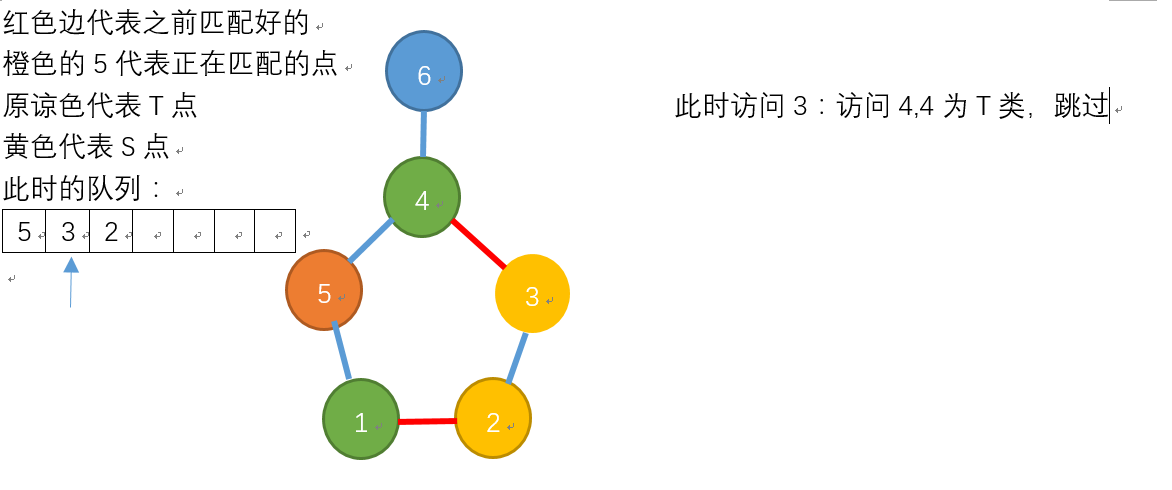
3号点的探索：



3号节点探测出来奇环：



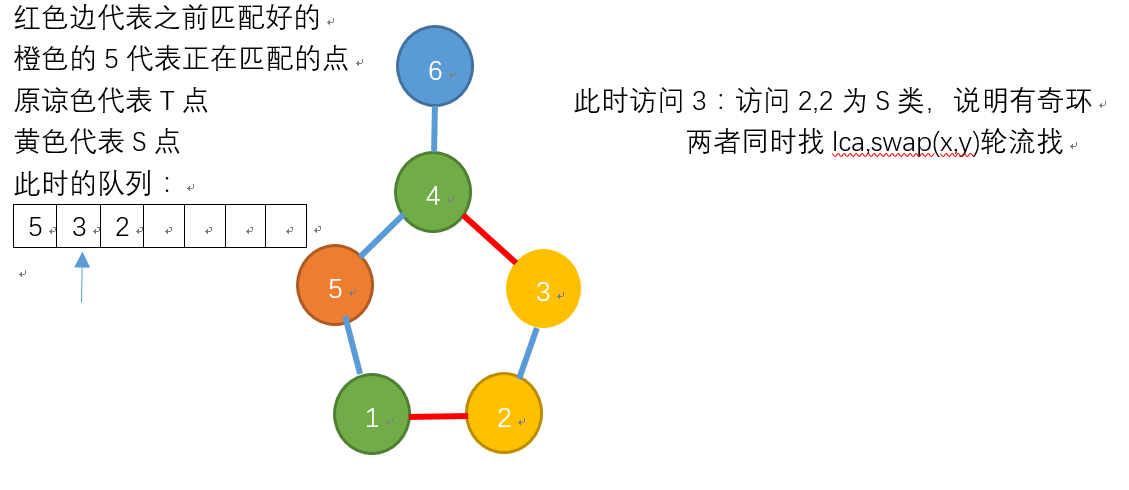
寻找lca,以及维护的信息，环中的id[] == 1的点入队（此处多了之前维护的pre[]的示例）:



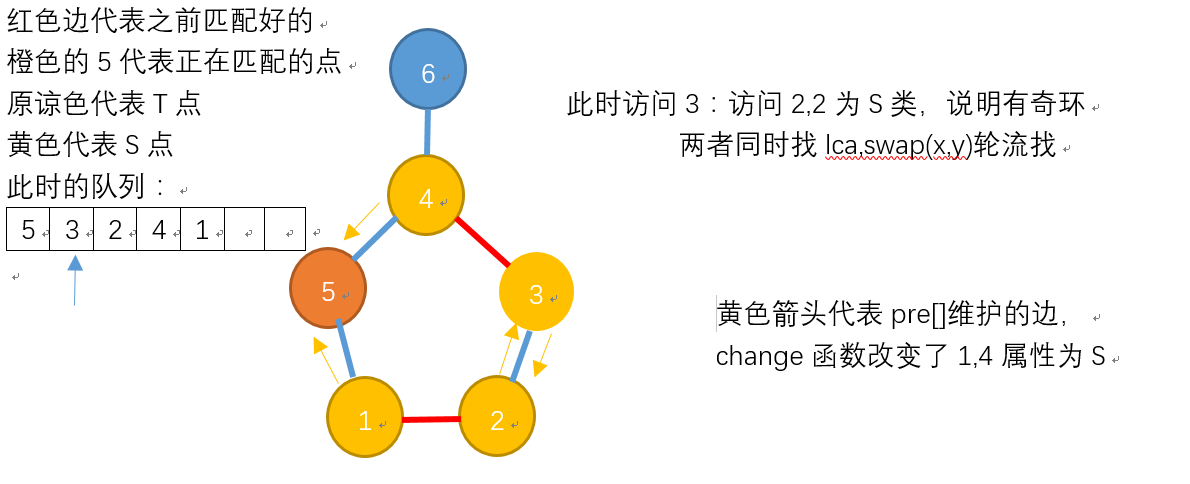
最终增广的结果，注意pre[]记录以及match[]两个数组记录了需要增广的边。两者交替进行：



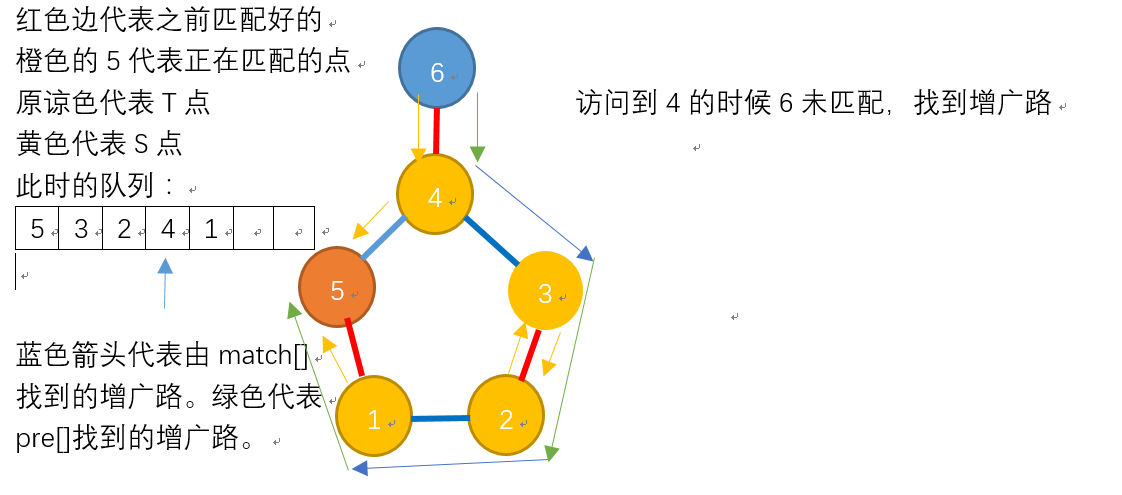
看完了上面的流程图，是不是有了新的理解呢？

偶环的例子

为什么遇到了偶环和二分图的最大匹配是一样的呢？因为它只要找到了增广路就会增广，不会出现奇环那样：即使里面的n-1(n为奇)个点已经匹配好了，但是依旧会增广。偶环里面的n个点最少会有n-1个节点匹配,（还有一个节点若依旧找到了增广路依旧会增广。）
偶环中的一个点被孤立的样子：



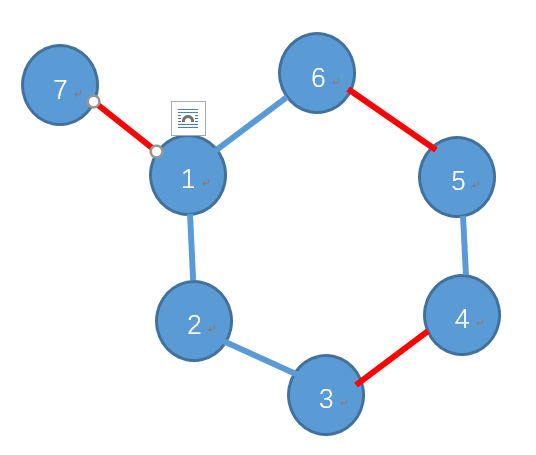
下面是具体的例子：

<一>初始状态，外点连接匹配点：



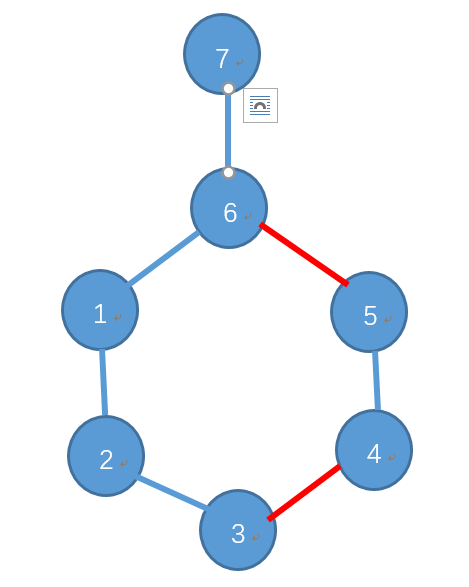
情况①：外面的点和已匹配点寻找增广：



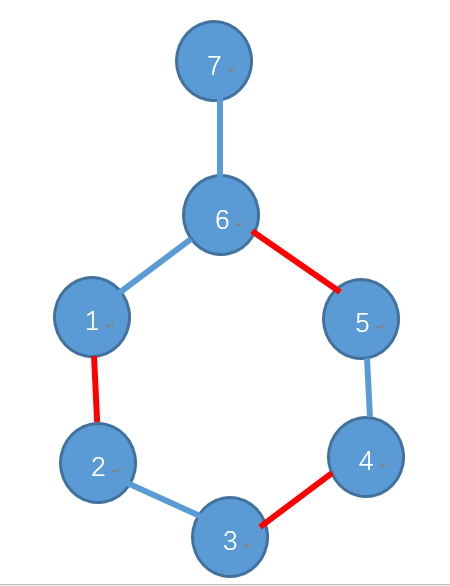
情况②：环内的两点可增广：



<二>初始状态，外点连接未匹配点：



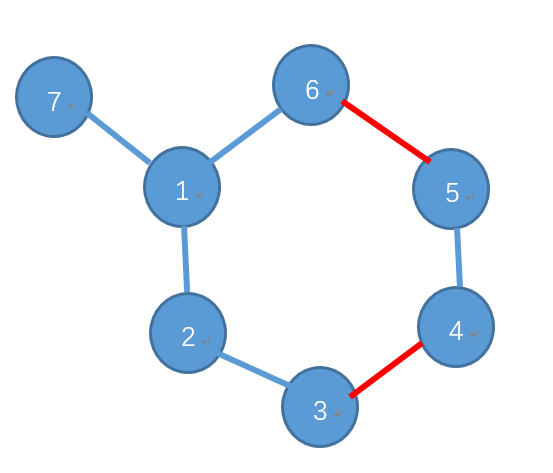
情况①：外点和环内的点直接可增广



情况②: 偶环内的连点直接匹配：



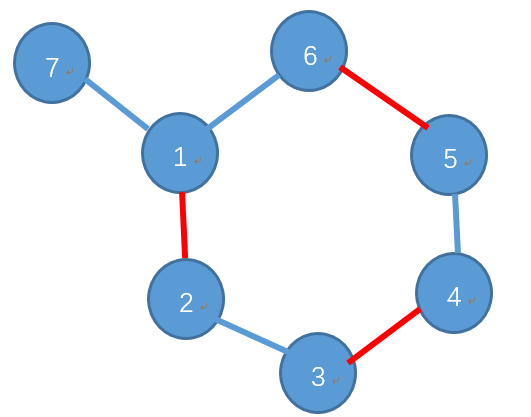
更多的例子，都可以构造，发现和二分图的最大匹配流程都是一样的：



AC代码

复杂度：O(\(n^3\))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
#include<cstdio>
#include<cstring>
#include <bits/stdc++.h>
using namespace std;
const int N=505*2;
const int M=124750*2;
int f[N];
struct qq
{
	int x,y;
	int last;
}s[M];
int num,last[N];
int n,m;
//链式前向星来存储图
void init (int x,int y)
{
	num++;
	s[num].x=x;s[num].y=y;
	s[num].last=last[x];
	last[x]=num;
}
int match[N];
int id[N];//这个点是什么点
//-1:没访问过  0:S点  1:T点
int q[N];//要扩展的队列————也就是我们要尝试帮谁换配偶
int pre[N];//在这次过程中,x的新配偶是谁
int Tim,vis[N];//对于lca的标记以及时间轴
int find (int x)
{
	if (f[x]==x) return f[x];
	f[x]=find(f[x]);
	return f[x];
}
int lca (int x,int y)//寻找lca
{
	Tim++;
	//cout<<"test "<<x<<" "<<y<<endl;
	while (vis[x]!=Tim)
	{
		if (x!=0)
		{
			x=find(x);//先找到花根
			if (vis[x]==Tim) return x;
			vis[x]=Tim;
			if (match[x]!=0) x=find(pre[match[x]]);
			//因为在之前我们知道，每一个S点的配偶(也就是T点)的pre 都是指向他的父亲的,于是就直接这么跳就可以了
			//还有要注意的是，一定要先去到花根，因为他们现在已经是一个点了，只有花根的pre才指向他们真正的父亲
			else x=0;
		}
		//cout<<"jiaohuan:"<<x<<" "<<endl;
		swap(x,y);
	}
	//cout<<"gen:"<<x<<endl;
	return x;
}
int st,ed;
void change (int x,int y,int k)//环  出现的是x---y的连边  已知根是k
{
    //cout<<x<<" "<<"suohuan"<<y<<endl;
	while (find(x)!=k)
	{
	    //cout<<"haha"<<x<<" "<<pre[x]<<endl;
		pre[x]=y;
		int z=match[x];
		id[z]=0;q[ed++]=z;if (ed>=N-1) ed=1;
		if (find(z)==z) f[z]=k;
		if (find(x)==x) f[x]=k;
		y=z;x=pre[y];
	}
}
void check (int X)//尽量帮助x寻找增广路
{
	for (int u=1;u<=n;u++) {f[u]=u;id[u]=-1;}
	st=1;ed=2;//模仿栈的两个指针的玩意来模拟queue，类似于AC自动机之类的
	q[st]=X;id[X]=0;
	while (st!=ed)
	{
		int x=q[st];
		for (int u=last[x];u!=-1;u=s[u].last)
		{
			int y=s[u].y;
			//cout<<"处理中的对子："<<x<<" "<<y<<" "<<match[5]<<endl;
			if (match[y]==0&&y!=X)
			//当然match[X]=0,但X(这次来寻找配偶的点)并不是一个可行的东西,所以不能算可行解
			{
//			    for(int i=1; i <=6; i++){
//                    cout<<pre[i]<<" ";
//			    }
//			    cout<<endl;
				pre[y]=x;//先假设他与x相连
				int last,t,now=y;
				while (now!=0)//当然，这次来的X的match是为0，要是能更新到0就是结束
				{
					t=pre[now];//now新的配偶
					last=match[t];//理所当然啦
					match[t]=now;match[now]=t;
					now=last;
					//cout<<"now:"<<now<<endl;
				}
				//cout<<"result: "<<x<<" "<<y<<" "<<match[5]<<endl;
				return ;
			}
			if (id[y]==-1)//找到一个没有访问过的点————进行扩展
			{
				id[y]=1;
				pre[y]=x;//先假设他与x相连
				id[match[y]]=0;q[ed++]=match[y];
				if (ed>=N-1) ed=1;
			}
			else if (id[y]==0&&find(x)!=find(y))//出现一个以前未处理过的奇环
			{
				int g=lca(x,y);
				change(x,y,g);change(y,x,g);
			}
		}
		st++;
		if (st>=N-1) st=1;
	}
}
int main()
{
	memset(vis,0,sizeof(vis));Tim=0;
	memset(match,0,sizeof(match));
	num=0;memset(last,-1,sizeof(last));
	scanf("%d%d",&n,&m);
	for (int u=1;u<=m;u++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		init(x,y);init(y,x);
	}
	for (int u=1;u<=6;u++)
		if (match[u]==0){
            check(u);
            //cout<<"233 "<<match[5]<<endl;
		}
	int ans=0;
	for (int u=1;u<=n;u++)
		if (match[u]!=0) ans++;
	printf("%d\n",ans/2);
	for (int u=1;u<=n;u++) printf("%d ",match[u]);
	return 0;
}

自己的一些理解

  • 不论是奇环还是偶环，环里面的点都能组成很大(不是最大)的匹配。
  • 若是奇环，最少也能组成\(\frac{n-1}{2}\)组匹配。现在我们要设计一种算法，看看剩下的那个点是否也能够利用。若奇环中的一个点能够和外面的路构成新的匹配，那么剩下的n-1一个节点就能两两匹配了，十分充分的利用了所有的点。
  • 若是偶环，至少n-1（n为偶数）参与匹配。即使剩余了一个点。剩余的那个点和旁边的点其实也可以匹配，只不过由于匹配的顺序，而被环外的点抢占了。因此，偶环无论怎样，它的所有点都是被充分的利用的。无需设计新的算法来求解。

参考的博客

有详细的流程
带花树名字由来
博客的标签很好

未解决的问题

赶快去刷题，总结自己的模板。
刷题推荐

本文标题:一般图的匹配

文章作者:Babydragon

发布时间:2017-10-09, 00:03:51

最后更新:2018-03-23, 13:35:58

原始链接:http://baolintian.github.io/2017/10/09/一般图的匹配-带花树算法/

许可协议: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

文章目录
  1. 1. 题目
  2. 2. 题解
  3. 3. 一般图最大匹配的算法流程
  4. 4. 奇环的例子
  5. 5. 偶环的例子
  6. 6. AC代码
  7. 7. 自己的一些理解
  8. 8. 参考的博客
  9. 9. 未解决的问题
{{ live2d() }}