输入
我们得到的是一个784个范围属于(0, 1)的图像点阵。然后设置两层调参的元胞,每层16个,最后是表示0~9的层,值越大表示代表该数的可能性越大。最后定义一个方差:方差越小表示与目标的预测越精确。我们需要的调节的参数有两种:\(w和b\),一个代表调节neutron的权重的边,另外一个表示偏度。总共需要调节的参数总数为:
\((784*16 + 16*16 + 16*10) + (16 + 16 + 10) = 13002\),前面的表示w的数目,后面表示b的数目。
其实不断训练的过程就是:调节13002个参数,使方差最小。若是多元的函数,我们会选择梯度下降法,在这个系列的视频中,采用的是back propagation(BP)算法来寻找最小值。
识别的过程
我们很自然的以为设置的第一层元胞是识别小的笔画,第二层识别第一层组合起来更大的笔画。最后一层是第二层笔画的组合。这样看起来合情合理。
但是时间上它生成了13002幅784像素的图,并且与现实吻合的很好,但是它的识别的过程完全是无规律的。不要把它想的太高端。
比如我们输入一幅噪点图,算法总能给我们一个结果,但实际上没有任何的数字。因此它的识别过程完全是无序的。
BP原理
此处应该有大量的公式以及符号说明,等有时间再补吧qaq.
线性的neutron时:

符号说明:
\(C_0\):训练的代价,即一个方差。越小表示越接近真实值。
\(y\):要么是0, 要么是1,。并且只有一个1.
\(W^{(L)}\):第\(L\)层的权重。
\(a^{(L)}\):表示neutron的值(激活值),它是连续的,并且属于(0, 1).
\(b^{(L)}\):偏差的系数(bias)。
\(\sigma()\):特殊函数,比如sigmoid函数。
当有多个neutron
只不过描述变量的时候多了一个下标。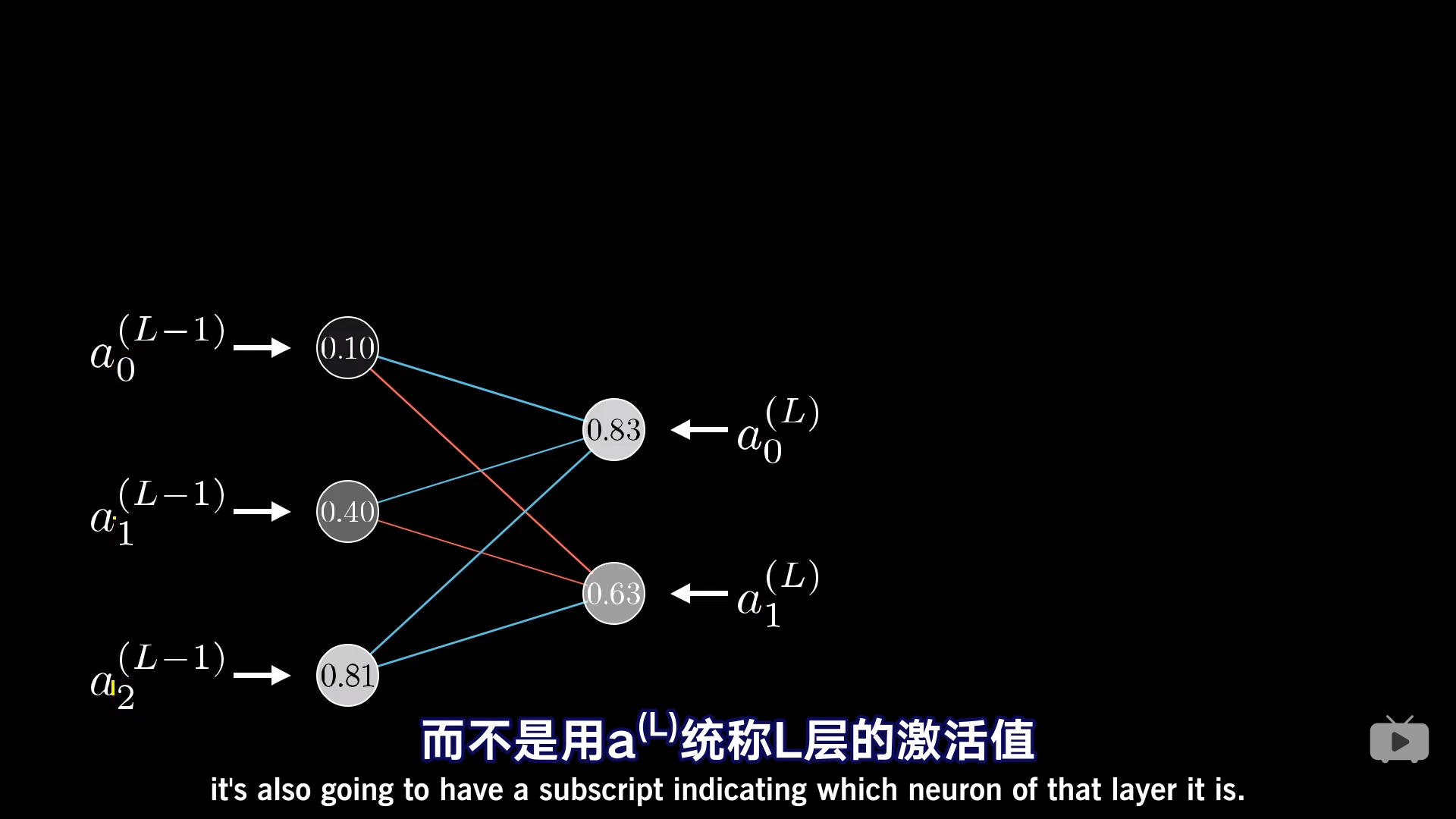
变量的说明: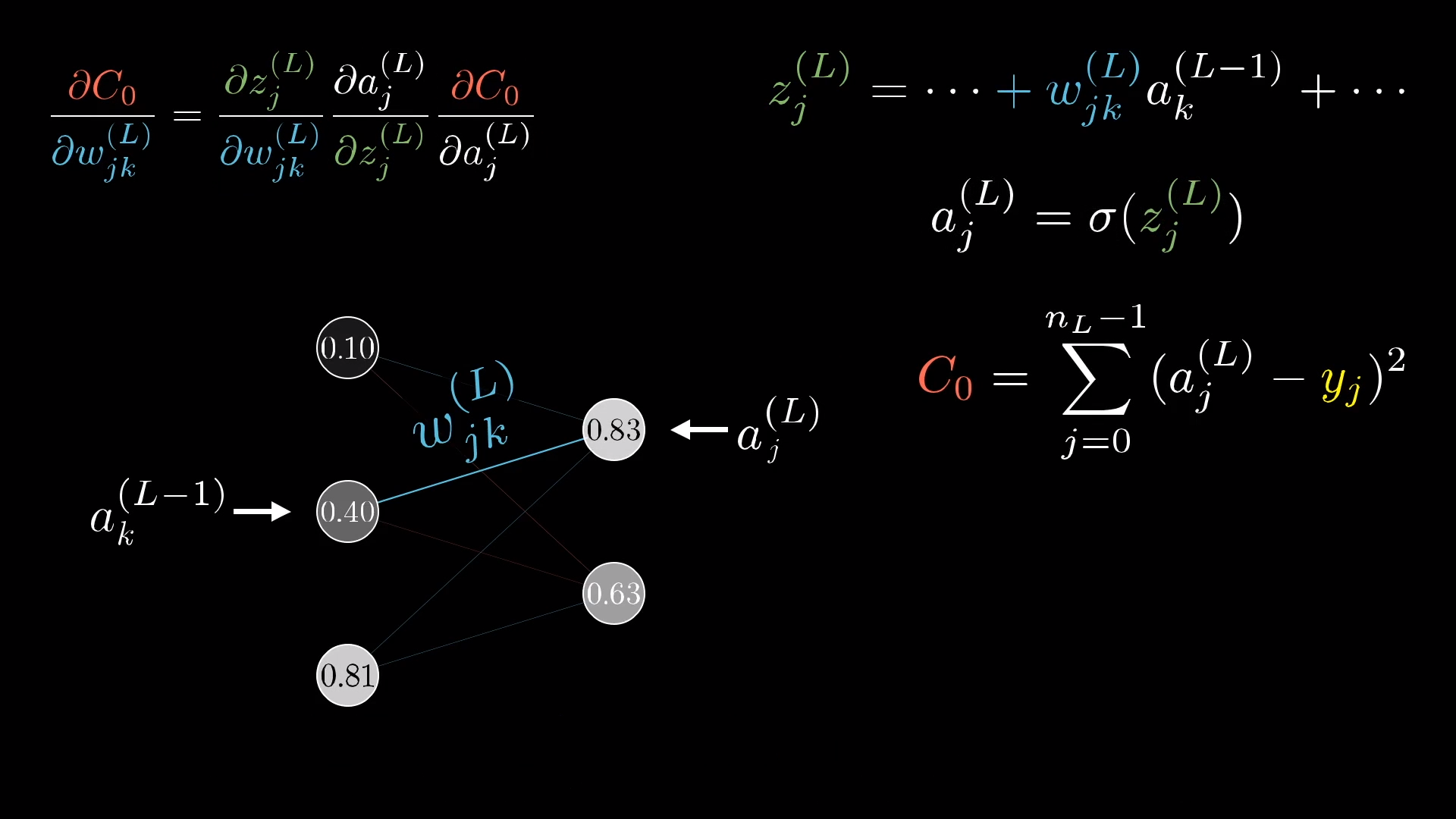
\(C_0 \):表示误差的代价,是方差。
\(a_{i}^{(L)}\):表示第L层的第i+1个激活值,注意比线性的多了一个下标。
\(W_{jk}^{(L)}\):第L-1层的第k个neutron和第L层的第j个neutron之间的权重.看似顺序有点不太对,实际上是第1集中定义的矩阵有关。
\(y_i\):只能取0或者1,表示结果。并且所有的y中只能有一个表示1,表示正确结果。
注意\(C_0\)对\(a_k^{(L-1)}\)的偏导的结果前面有一个累加号,因为\(a_k^{(L-1)}\)对后面一层的所有的\(a_i^{(L)}\)都有影响。