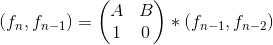模板积累
FAQ
- 绝大部分的RE错误来源于数组开的过小
- 注意整数除以整数的时候乘以1.0,除非要是用整除的含义(拓展欧几里得)
- 使用并查集的时候最后要扫一遍,使路径压缩。
- 时刻注意数字的范围,如果题目中出现了long long 一定要高度的重视,因为很有可能会被坑
- 开比较大的栈:#pragma comment(linker, “/STACK:102400000,102400000”)
快速读入挂
有时候并不一定就很快emmm
1 2 3 4 5 6 7 8 9 10 11 12
| ll readll(){ ll x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int readint(){ int x=0,f=1;char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch))x=x*10+ch-'0',ch=getchar(); return f*x; }
|
c++高精度
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403
| #include<string> #include<iostream> #include<iosfwd> #include<cmath> #include<cstring> #include<stdlib.h> #include<stdio.h> #include<cstring> #define MAX_L 2005 using namespace std; class bign { public: int len, s[MAX_L]; bign(); bign(const char*); bign(int); bool sign; string toStr() const; friend istream& operator>>(istream &,bign &); friend ostream& operator<<(ostream &,bign &); bign operator=(const char*); bign operator=(int); bign operator=(const string); bool operator>(const bign &) const; bool operator>=(const bign &) const; bool operator<(const bign &) const; bool operator<=(const bign &) const; bool operator==(const bign &) const; bool operator!=(const bign &) const; bign operator+(const bign &) const; bign operator++(); bign operator++(int); bign operator+=(const bign&); bign operator-(const bign &) const; bign operator--(); bign operator--(int); bign operator-=(const bign&); bign operator*(const bign &)const; bign operator*(const int num)const; bign operator*=(const bign&); bign operator/(const bign&)const; bign operator/=(const bign&); bign operator%(const bign&)const; bign factorial()const; bign Sqrt()const; bign pow(const bign&)const; void clean(); ~bign(); }; #define max(a,b) a>b ? a : b #define min(a,b) a<b ? a : b bign::bign() { memset(s, 0, sizeof(s)); len = 1; sign = 1; } bign::bign(const char *num) { *this = num; } bign::bign(int num) { *this = num; } string bign::toStr() const { string res; res = ""; for (int i = 0; i < len; i++) res = (char)(s[i] + '0') + res; if (res == "") res = "0"; if (!sign&&res != "0") res = "-" + res; return res; } istream &operator>>(istream &in, bign &num) { string str; in>>str; num=str; return in; } ostream &operator<<(ostream &out, bign &num) { out<<num.toStr(); return out; } bign bign::operator=(const char *num) { memset(s, 0, sizeof(s)); char a[MAX_L] = ""; if (num[0] != '-') strcpy(a, num); else for (int i = 1; i < strlen(num); i++) a[i - 1] = num[i]; sign = !(num[0] == '-'); len = strlen(a); for (int i = 0; i < strlen(a); i++) s[i] = a[len - i - 1] - 48; return *this; } bign bign::operator=(int num) { char temp[MAX_L]; sprintf(temp, "%d", num); *this = temp; return *this; } bign bign::operator=(const string num) { const char *tmp; tmp = num.c_str(); *this = tmp; return *this; } bool bign::operator<(const bign &num) const { if (sign^num.sign) return num.sign; if (len != num.len) return len < num.len; for (int i = len - 1; i >= 0; i--) if (s[i] != num.s[i]) return sign ? (s[i] < num.s[i]) : (!(s[i] < num.s[i])); return !sign; } bool bign::operator>(const bign&num)const { return num < *this; } bool bign::operator<=(const bign&num)const { return !(*this>num); } bool bign::operator>=(const bign&num)const { return !(*this<num); } bool bign::operator!=(const bign&num)const { return *this > num || *this < num; } bool bign::operator==(const bign&num)const { return !(num != *this); } bign bign::operator+(const bign &num) const { if (sign^num.sign) { bign tmp = sign ? num : *this; tmp.sign = 1; return sign ? *this - tmp : num - tmp; } bign result; result.len = 0; int temp = 0; for (int i = 0; temp || i < (max(len, num.len)); i++) { int t = s[i] + num.s[i] + temp; result.s[result.len++] = t % 10; temp = t / 10; } result.sign = sign; return result; } bign bign::operator++() { *this = *this + 1; return *this; } bign bign::operator++(int) { bign old = *this; ++(*this); return old; } bign bign::operator+=(const bign &num) { *this = *this + num; return *this; } bign bign::operator-(const bign &num) const { bign b=num,a=*this; if (!num.sign && !sign) { b.sign=1; a.sign=1; return b-a; } if (!b.sign) { b.sign=1; return a+b; } if (!a.sign) { a.sign=1; b=bign(0)-(a+b); return b; } if (a<b) { bign c=(b-a); c.sign=false; return c; } bign result; result.len = 0; for (int i = 0, g = 0; i < a.len; i++) { int x = a.s[i] - g; if (i < b.len) x -= b.s[i]; if (x >= 0) g = 0; else { g = 1; x += 10; } result.s[result.len++] = x; } result.clean(); return result; } bign bign::operator * (const bign &num)const { bign result; result.len = len + num.len; for (int i = 0; i < len; i++) for (int j = 0; j < num.len; j++) result.s[i + j] += s[i] * num.s[j]; for (int i = 0; i < result.len; i++) { result.s[i + 1] += result.s[i] / 10; result.s[i] %= 10; } result.clean(); result.sign = !(sign^num.sign); return result; } bign bign::operator*(const int num)const { bign x = num; bign z = *this; return x*z; } bign bign::operator*=(const bign&num) { *this = *this * num; return *this; } bign bign::operator /(const bign&num)const { bign ans; ans.len = len - num.len + 1; if (ans.len < 0) { ans.len = 1; return ans; } bign divisor = *this, divid = num; divisor.sign = divid.sign = 1; int k = ans.len - 1; int j = len - 1; while (k >= 0) { while (divisor.s[j] == 0) j--; if (k > j) k = j; char z[MAX_L]; memset(z, 0, sizeof(z)); for (int i = j; i >= k; i--) z[j - i] = divisor.s[i] + '0'; bign dividend = z; if (dividend < divid) { k--; continue; } int key = 0; while (divid*key <= dividend) key++; key--; ans.s[k] = key; bign temp = divid*key; for (int i = 0; i < k; i++) temp = temp * 10; divisor = divisor - temp; k--; } ans.clean(); ans.sign = !(sign^num.sign); return ans; } bign bign::operator/=(const bign&num) { *this = *this / num; return *this; } bign bign::operator%(const bign& num)const { bign a = *this, b = num; a.sign = b.sign = 1; bign result, temp = a / b*b; result = a - temp; result.sign = sign; return result; } bign bign::pow(const bign& num)const { bign result = 1; for (bign i = 0; i < num; i++) result = result*(*this); return result; } bign bign::factorial()const { bign result = 1; for (bign i = 1; i <= *this; i++) result *= i; return result; } void bign::clean() { if (len == 0) len++; while (len > 1 && s[len - 1] == '\0') len--; } bign bign::Sqrt()const { if(*this<0)return -1; if(*this<=1)return *this; bign l=0,r=*this,mid; while(r-l>1) { mid=(l+r)/2; if(mid*mid>*this) r=mid; else l=mid; } return l; } bign::~bign() { } bign num[105]; int main() { num[1] = 1, num[2] = 5; int n; cin>>n; for(int i=3; i<=n; i++){ num[i] = num[i-1]*3-num[i-2]+2; } cout << num[n] << endl; return 0; }
|
int128的读入
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54
| #include <bits/stdc++.h> using namespace std; template <class T> inline bool scan_d(T & ret) { char c; int sgn; if(c = getchar(), c == EOF)return false; while(c != '-' && (c < '0' || c > '9'))c = getchar(); sgn = (c == '-') ? -1 : 1; ret = (c == '-') ? 0 : (c - '0'); while(c = getchar(), c >= '0' && c <= '9') ret = ret * 10 + (c - '0'); ret *= sgn; return true; } #ifdef Cpp11 template <class T, class ... Args> inline bool scan_d(T & ret, Args & ... args) { scan_d(ret); scan_d(args...); } #define cin.tie(0); cin.tie(nullptr); #define cout.tie(0); cout.tie(nullptr); #endif inline bool scan_ch(char &ch) { if(ch = getchar(), ch == EOF)return false; while(ch == ' ' || ch == '\n')ch = getchar(); return true; } template <class T> inline void out_number(T x) { if(x < 0) { putchar('-'); out_number(- x); return ; } if(x > 9)out_number(x / 10); putchar(x % 10 + '0'); } int main() { __int128 a, b; scan_d(a), scan_d(b); out_number(a + b); puts(""); return 0; }
|
python 读入
1 2 3 4 5 6 7 8 9 10
| import math if __name__ == '__main__': try: while True: a, b, c = map(int, input().split()) print(pow(a, int(pow(b, c, int(1e9 + 6))), int(1e9 + 7))) except EOFError: pass
|
读取带有空格的字符串
1 2 3 4 5 6 7
| //method 1 string str; getline(cin, str); //method 2 char str[maxn]; gets(str);
|
adptive Simpson’s rule
为什么求sin(x)/x就会挂掉啊不知道MATLAB能不能求出来这种形式的积分,明天试试。
还有三重积分球体积怎么用数值分析的方法来求?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
| #include <bits/stdc++.h> using namespace std; const double PI = acos(-1.0); double F(double x){ return sin(x); } double simpson(double a, double b){ double c = a+(b-a)/2; return (F(a)+4*F(c)+F(b))*(b-a)/6; } double asr(double a, double b, double eps, double A){ double c = a+(b-a)/2; double L = simpson(a, c), R = simpson(c, b); if(fabs(L+R-A) <= 15*eps) return L+R+(L+R-A)/15.0; return asr(a, c, eps/2, L)+asr(c, b, eps/2, R); } double asr(double a, double b, double eps){ return asr(a, b, eps, simpson(a, b)); } int main() { double s = asr(0, PI, 1e-5); cout<<s<<endl; return 0; }
|
二分图匹配
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
| #include <bits/stdc++.h> using namespace std; const int maxn = 505; vector<int> G[maxn*2]; int match[maxn*2]; int used[maxn*2]; int n, m, l; void add_edge(int u, int v) { G[u].push_back(v); G[v].push_back(u); } bool dfs(int v){ used[v] = true; for(int i=0; i<G[v].size(); i++){ int u = G[v][i], w = match[u]; if(w == -1 || !used[w]&&dfs(w)){ match[u] = v; match[v] = u; return true; } } return false; } void solve(){ int ans = 0; memset(match, -1, sizeof(match)); for(int v=0; v<=n; v++){ if(match[v] == -1){ memset(used, 0, sizeof(used)); if(dfs(v)) ans++; } } for(int v=500; v<=m+500; v++){ if(match[v] == -1){ memset(used, 0, sizeof(used)); if(dfs(v)) ans++; } } printf("%d\n", ans); } int main() { while(~scanf("%d%d", &n, &m)){ for(int i=0 ;i<maxn*2; i++) G[i].clear(); scanf("%d", &l); for(int i=1; i<=l; i++){ int u, v; scanf("%d%d", &u, &v); add_edge(u, v+500); } solve(); } return 0; }
|
Dinic算法求最大流
接口
n:节点的个数
m:边的个数
s:起始点(源点)
t:终点(汇点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85
| #include <cstdio> #include <cstring> #include <algorithm> #include <vector> #include <queue> using namespace std; const int maxn = 205; const int INF = 1e9+10; struct Edge{ int to, cap, rev; }; vector<Edge> G[maxn]; int cnt[maxn]; int level[maxn]; int s, t; int n, m; void add_edge(int u, int v, int cap){ G[u].push_back(Edge{v, cap, G[v].size()}); G[v].push_back(Edge{u, 0, G[u].size()-1}); } void bfs(int s){ memset(level, -1, sizeof(level)); queue<int> q; q.push(s); level[s] = 0; while(!q.empty()){ int v = q.front(); q.pop(); for(int i=0; i<G[v].size(); i++){ Edge& e = G[v][i]; if(e.cap>0&&level[e.to]<0){ level[e.to] = level[v]+1; q.push(e.to); } } } } int dfs(int v, int t, int flow){ if(v == t) return flow; for(int& i=cnt[v]; i<G[v].size(); i++){ Edge& e = G[v][i]; if(e.cap>0&&level[v]<level[e.to]){ int d = dfs(e.to, t, min(flow, e.cap)); if(d>0){ e.cap -= d; G[e.to][e.rev].cap += d; return d; } } } return 0; } int max_flow(int s, int t){ int flow = 0; for(;;){ bfs(s); if(level[t]<0) return flow; int f; memset(cnt, 0, sizeof(cnt)); while((f = dfs(s, t, INF))>0){ flow+=f; } } } int main() { while(~scanf("%d%d", &n, &m)){ for(int i=0; i<=n; i++) G[i].clear(); int u, v, cap; for(int i=0; i<m; i++){ scanf("%d %d %d", &u, &v, &cap); add_edge(u, v, cap); } s = 1; t = n; printf("%d\n", max_flow(s, t)); } return 0; }
|
最小费用流最新模板
费用是float类型的。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110
| #include <cstdio> #include <algorithm> #include <cstring> #include <vector> #include <queue> #include <cmath> #include <iostream> #define double float using namespace std; const int maxn = 200+10; namespace mincostflow { const int INF=0x3f3f3f3f; struct node { int to; int cap; double cost; int rev; node(int t=0,int c=0,double _c=0,int n=0): to(t),cap(c),cost(_c),rev(n) {}; }; vector<node> edge[maxn]; void addedge(int from,int to,int cap,double cost) { edge[from].push_back(node(to,cap,cost,edge[to].size())); edge[to].push_back(node(from,0,-cost,edge[from].size()-1)); } double dis[maxn]; bool mark[maxn]; void spfa(int s,int t,int n) { for(int i=0; i<=n+2; i++) dis[i] = double (INF); memset(mark+1,0,n*sizeof(bool)); static int Q[maxn],ST,ED; dis[s]=0; ST=ED=0; Q[ED++]=s; while (ST!=ED) { int v=Q[ST]; mark[v]=0; if ((++ST)==maxn) ST=0; for (node &e:edge[v]) { if (e.cap>0&&dis[e.to]>dis[v]+e.cost) { dis[e.to]=dis[v]+e.cost; if (!mark[e.to]) { if (ST==ED||dis[Q[ST]]<=dis[e.to]) { Q[ED]=e.to,mark[e.to]=1; if ((++ED)==maxn) ED=0; } else { if ((--ST)<0) ST+=maxn; Q[ST]=e.to,mark[e.to]=1; } } } } } } int cur[maxn]; int dfs(int x,int t,int flow) { if (x==t||!flow) return flow; int ret=0; mark[x]=1; for (int &i=cur[x];i<(int)edge[x].size();i++) { node &e=edge[x][i]; if (!mark[e.to]&&e.cap) { if (dis[x]+e.cost==dis[e.to]) { int f=dfs(e.to,t,min(flow,e.cap)); e.cap-=f; edge[e.to][e.rev].cap+=f; ret+=f; flow-=f; if (flow==0) break; } } } mark[x]=0; return ret; } pair<int,double> min_costflow(int s,int t,int n) { int ret=0; double ans=0; int flow = INF; while (flow) { spfa(s,t,n); if (dis[t]==double(INF)) break; memset(cur+1,0,n*sizeof(int)); double len=dis[t]; int f; while ((f=dfs(s,t,flow))>0) ret+=f,ans+=len*f,flow-=f; } return make_pair(ret,ans); } void init(int n) { int i; for (int i = 1; i <= n; i++) edge[i].clear(); } } int n, m; using namespace mincostflow; int ss, tt; double e = 2.718281828459045; int main(int argc, char const *argv[]) { int _; scanf("%d", &_); while(_--){ scanf("%d %d", &n, &m); init(n+2); int x, y, z; double s; ss=1, tt = n+2; for(int i=1; i<=n; i++) { scanf("%d%d", &x, &y); if(x) addedge(ss, i + 1, x, 0); if(y) addedge(i + 1, tt, y, 0); } for (int i = 1; i <= m; i++) { scanf("%d %d %d %f", &x, &y, &z, &s); if(z)addedge(x + 1, y + 1, z-1, -log(1.0 - s)), addedge(x + 1, y + 1, 1, 0.0); } pair<int,double > ans = min_costflow(ss, tt, n+2); printf("%.2f\n", 1.0-pow(e, -ans.second)); } return 0; }
|
链式前向星来存图
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
| #include <bits/stdc++.h> using namespace std; const int maxn = 4e5+100; struct node{ int to, next, weight; }edge[maxn]; int cnt; int head[maxn]; int n; void add(int u, int v, int weight) { edge[cnt].to = v; edge[cnt].weight = weight; edge[cnt].next = head[u]; head[u] = cnt++; } int main() { while(cin>>n){ cnt=0, memset(head, -1, sizeof(head)); for(int i=0; i<n-1; i++){ int u, v, weight; cin>>u>>v>>weight; add(u, v, weight); add(v, u, weight); } for(int i=1; i<=n; i++){ for(int j=head[i]; j!=-1; j = edge[j].next){ cout<<edge[j].to<<" "; } cout<<endl; } } return 0; }
|
快速幂
快速幂
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
| #include <cstdio> using namespace std; typedef long long ll; ll a, b, c; ll pow_mod(ll a, ll b, ll mod){ ll ans = 1; while(b){ if(b&1){ ans = ans*a%mod; } a = a*a%mod; b>>=1; } return ans; } int main(){ while(~scanf("%I64d%I64d%I64d", &a, &b, &c)){ printf("%I64d\n", pow_mod(a, b, c)); } return 0; }
|
矩阵快速幂
斐波那契数列
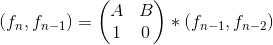
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55
| #include <cstdio> #include <cstring> using namespace std; typedef long long ll; const int maxn = 2; const int mod = 7; int A, B, n; struct Mat{ int mat[maxn][maxn]; Mat(){ memset(mat, 0, sizeof(mat)); } }; Mat mul(Mat a, Mat b, int n){ Mat ans; for(int i=0; i<n; i++){ for(int k=0; k<n; k++){ for(int j=0; j<n; j++){ ans.mat[i][j] = (ans.mat[i][j]+a.mat[i][k]*b.mat[k][j])%mod; } } } return ans; } Mat pow_mat(Mat a, int b, int n){ Mat ans; for(int i=0; i<n; i++)ans.mat[i][i] = 1; while(b){ if(b&1){ ans = mul(a, ans, n); } a = mul(a, a, n); b>>=1; } return ans; } int main(){ while(~scanf("%d%d%d", &A, &B, &n)&&A+B+n!=0){ Mat a; a.mat[0][0] = A, a.mat[0][1] = B, a.mat[1][0] = 1, a.mat[1][1] = 0; if(n <= 2){ printf("%d\n", 1); } else{ Mat ans = pow_mat(a, n-2, 2); int temp = (ans.mat[0][0]+ans.mat[0][1])%mod; printf("%d\n", temp); } } return 0; }
|
求逆元
拓展欧几里德求解逆元
用拓展欧几里德来求解逆元的时候,需要\(gcd(b, mod)=1\)。
拓展欧几里德的模板题
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
| #include <bits/stdc++.h> using namespace std; typedef long long ll; const int mod = 9973; void extgcd(ll a,ll b,ll& d,ll& x,ll& y){ if(!b){ d=a; x=1; y=0;} else{ extgcd(b,a%b,d,y,x); y-=x*(a/b); } } ll inverse(ll a,ll n){ ll d,x,y; extgcd(a,n,d,x,y); return d==1?(x+n)%n:-1; } int T; int n, b; int main() { scanf("%d", &T); for(int i=0; i<T; i++){ scanf("%d%d", &n, &b); ll inver = inverse(b, mod); int ans = inver*n%mod; printf("%d\n", ans); } return 0; }
|
费马小定理求解逆元
若被摸的数p为素数的时候,有拓展费马小定理证明:
\(a^{p-1}\equiv 1mod p\)
那么a的逆元就为\(a^{p-2}\).
快速幂搞一下就行了
一般的求解。

一般求解方法:
}{b})
但是p*b的值往往是比较的大的,有时候会溢出就不知道怎么弄了。(看后面的有关的一道数论的题目)
c++中一些优秀的函数
strstr
可以部分的取代kmp算法,但是不能统计子串的个数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
| #include <bits/stdc++.h> using namespace std; const int maxn = 1e3+10; char pattern[maxn]; char text[maxn<<4]; int main() { char *ptr; while(~scanf("%s%s", pattern, text)){ ptr = strstr(text, pattern); int len = strlen(pattern); if(ptr != NULL){ char ans[maxn]; for(int i=0; i<len; i++){ ans[i] = ptr[i]; } ans[len] = '\0'; printf("%s\n", ans); } else{ printf("-1\n"); } } return 0; }
|
unique
使用unique之前要先对数组进行相应的排序,然后求得不同数字的个数。
unique不改变原来数组
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
| #include <bits/stdc++.h> using namespace std; int main(){ int num[20]; for(int i=0; i<10; i++){ num[i] = i+1; } for(int i=10; i<20; i++){ num[i] = i-9; } sort(num, num+20); int sz = unique(num, num+20)-num; cout<<sz<<endl; return 0; }
|
lower_bound()
返回第一个大于等于这个值的下标(下标是从0开始的)
1 2
| int num[10] = {1, 2, 3, 4, 5, 5, 6, 7, 8, 9}; printf("%d\n", lower_bound(num, num+10, 5)-num);
|
upper_bound()
返回第一个大于这个值的下标
1 2
| int num[10] = {1, 2, 3, 4, 5, 5, 6, 7, 8, 9}; printf("%d\n", upper_bound(num, num+10, 5)-num);
|
make_heap&&distance
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
| #include <bits/stdc++.h> using namespace std; const int maxn = 55; int n; int num[maxn]; vector<int> heap; int main() { scanf("%d", &n); for(int i=0; i<n; i++){ scanf("%d", &num[i]); heap.push_back(num[i]); } make_heap(heap.begin(), heap.end(), greater<int>() ); for(vector<int>::iterator it = heap.begin(); it!=heap.end(); it++){ printf("%d ", *it); } printf("\n"); return 0; } #include <bits/stdc++.h> using namespace std; const int maxn = 1e3+10; vector<int> num; int dis(int number){ return distance(num.begin(), find(num.begin(), num.end(), number)); } int main(){ int n; for(int i=1; i<=10; i++){ num.push_back(i); } cout<<dis(5)<<endl; }
|
bitset
bitset的各种操作
高中OIer真的是惹不起,太强了。初中就已经到达了我现在的水平,真的是好惭愧啊。
bitset的长度在刚开始的时候就已经定义好了
priority_queue
符号重载后面加const的原因
简单来说在这个函数里面不能修改任何的数据,否则就会报错,降低错误率。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
| #include <bits/stdc++.h> using namespace std; struct Node{ string name; int top; friend bool operator < (Node a, Node b){ return a.top>b.top; } }; priority_queue<Node> pq; struct cmp{ bool operator () (Node a, Node b){ if(a.top!=b.top) return a.top>b.top; } }; priority_queue<Node, vector<Node>, cmp> pq2; int main(){ pq2.push(Node{"tian", 2}); pq2.push(Node{"bao", 1}); pq2.push(Node{"lin", 3}); Node temp = pq2.top(); cout<<temp.name<<" "<<temp.top<<endl; return 0; }
|
树状数组
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
| #include <bits/stdc++.h> using namespace std; const int maxn = 1e3+10; int lowbit(int x){ return x&-x; } int num[maxn]; int c[maxn]; int n; void update(int x, int val){ while(x<=n){ c[x] += val; x += lowbit(x); } } int sum(int x){ int ans = 0; while(x>0){ ans += c[x]; x -= lowbit(x); } return ans; } int main(){ while(~scanf("%d", &n)){ for(int i=1; i<=n; i++){ scanf("%d", &num[i]); } for(int i=1; i<=n; i++){ update(i, num[i]); } for(int i=1; i<=n; i++){ printf("%d: %d\n", i, sum(i)); } } return 0; }
|
分治求逆序对的个数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
| ll merge_count(vector<int> &a){ int n = a.size(); if(n<=1) return 0; ll cnt = 0; vector<int> b(a.begin(), a.begin()+n/2); vector<int> c(a.begin()+n/2, a.end()); cnt += merge_count(b); cnt += merge_count(c); int ai = 0, bi = 0, ci=0; while(ai<n){ if(bi<b.size()&&(ci == c.size()||b[bi]<=c[ci])){ a[ai++] = b[bi++]; } else{ cnt += n/2-bi; a[ai++] = c[ci++]; } } return cnt; }
|
KMP算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
| #include <bits/stdc++.h> using namespace std; const int maxn = 1e3+10; int nexT[maxn]; char text[maxn]; char pattern[maxn]; int len1, len2; void get_next(){ nexT[0] = -1; int j = -1; for(int i=1; i<len2; i++){ while(j!=-1&&pattern[i]!=pattern[j+1]){ j = nexT[j]; } if(pattern[i] == pattern[j+1]){ j++; } nexT[i] = j; } } int KMP(){ get_next(); int j=-1; int ans = 0; for(int i=0; i<len1; i++){ while(j!=-1&&text[i]!=pattern[j+1]){ j = nexT[j]; } if(text[i] == pattern[j+1]){ j++; } if(j == len2-1){ ans++; j = nexT[j]; } } return ans; } int main() { while(~scanf("%s%s", text, pattern)){ len1 = strlen(text); len2 = strlen(pattern); printf("%d\n", KMP()); } return 0; }
|
二分图的染色问题
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39
| #include <bits/stdc++.h> using namespace std; const int maxn = 1e3+10; int color[maxn]; vector<int> G[maxn]; int n, m; bool bipartite(int u){ for(int i=0; i<G[u].size(); i++){ int v = G[u][i]; if(color[v]&&color[v] == color[u]) return false; if(!color[v]){ color[v] = 3 - color[u]; if(!bipartite(v)) return false; } } return true; } int main() { while(~scanf("%d%d", &n, &m)){ for(int i=0; i<n; i++) G[i].clear(); memset(color, 0, sizeof(color)); int u, v; for(int i=0; i<m; i++){ scanf("%d%d", &u, &v); G[u].push_back(v); G[v].push_back(u); } if(bipartite(0)){ printf("YES\n"); } else{ printf("NO\n"); } } return 0; }
|
割顶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64
| #include <bits/stdc++.h> using namespace std; const int maxn = 1e3+10; int n, m; vector<int> G[maxn]; int dfs_clock; int pre[maxn], low[maxn]; bool iscut[maxn]; int dfs(int u, int fa){ int lowu = pre[u] = ++dfs_clock; int child = 0; for(int i=0; i<G[u].size(); i++){ int v = G[u][i]; if(!pre[v]){ child++; int lowv = dfs(v, u); lowu = min(lowv, lowu); if(lowv>=pre[u]){ iscut[u] = true; } } else if(pre[u]>pre[v]&&fa!=v){ lowu = min(lowu, pre[v]); } } if(fa<0 &&child == 1) iscut[u] = false; low[u] = lowu; return lowu; } int main() { while(~scanf("%d%d", &n, &m)){ for(int i=0; i<n; i++) G[i].clear(); memset(iscut, 0, sizeof(iscut)); memset(pre, 0, sizeof(pre)); int u, v; for(int i=0; i<m; i++){ scanf("%d%d", &u, &v); G[u].push_back(v); G[v].push_back(u); } for(int i=0; i<n; i++){ if(!pre[i]) dfs(i, -1); } for(int i=0; i<n; i++){ printf("%d ", iscut[i]); } printf("\n"); } return 0; }
|
树的三序
还差一个层序遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114
| #include <bits/stdc++.h> using namespace std; const int maxn = 1e3+10; int pre[maxn]; int in[maxn]; int post[maxn]; int n; struct Node{ int data; Node* lchild; Node* rchild; Node(){ this->data = -1; this->lchild = this->rchild = NULL; } }; Node* build_post(int prel, int prer, int inl, int inr){ if(prer<prel) return NULL; Node* root = new Node; root->data = pre[prel]; int temp = pre[prel]; int k; for(k=inl; k<=inr; k++){ if(temp == in[k]) break; } int numleft = k-inl; root->lchild = build_post(prel+1, prel+numleft, inl, k-1); root->rchild = build_post(prel+numleft+1, prer, k+1, inr); return root; } Node* build_pre(int postl, int postr, int inl, int inr){ if(postr<postl) return NULL; Node* root = new Node; root->data = post[postr]; int temp = pre[postr]; int k; for(k=inl; k<=inr; k++){ if(temp == in[k]) break; } int numleft = k-inl; root->lchild = build_pre(postl, postl+numleft-1, inl, k-1); root->rchild = build_pre(postl+numleft, postr-1, k+1, inr); return root; } void post_order(Node* root){ if(root == NULL) return; post_order(root->lchild); post_order(root->rchild); printf("%d", root->data); } void pre_order(Node* root){ if(root == NULL) return; printf("%d", root->data); pre_order(root->lchild); pre_order(root->rchild); } void layer_order(Node *root){ queue<Node*> q; q.push(root); while(!q.empty()){ Node *temp = q.front(); q.pop(); printf("%d ", temp->data); if(temp->lchild != NULL) q.push(temp->lchild); if(temp->rchild != NULL) q.push(temp->rchild); } } int main() { int type; printf("请输入个数n以及所得到的序列:\n1.先序和中序\n2.中序和后序\n"); while(~scanf("%d", &type)){ printf("请输入数组的大小\n"); scanf("%d", &n); if(type == 1){ for(int i=0; i<n; i++) scanf("%d", &pre[i]); for(int i=0; i<n; i++) scanf("%d", &in[i]); Node* root = build_post(0, n-1, 0, n-1); post_order(root); printf("\n"); } else if(type == 2){ for(int i=0; i<n; i++) scanf("%d", &post[i]); for(int i=0; i<n; i++) scanf("%d", &in[i]); Node* root = build_pre(0, n-1, 0, n-1); printf("444\n"); pre_order(root); printf("\n"); } else{ printf("你是不是想捣乱!\n"); break; } } return 0; }
|
逆元
要求\(a\lt n\), 并且gcd(a, n) == 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
| typedef long long ll; ll ex_gcd(ll a, ll b, ll &x, ll &y){ if(a==0 && b==0) return -1; if(b == 0){ x=1, y=0; return a; } ll d = ex_gcd(b, a%b, y, x); y -= a/b*x; return d; } ll inv(ll a, ll n){ ll x, y; ll d = ex_gcd(a, n, x, y); if(d == 1) return (x%n+n)%n; else return -1; }
|
求组合数
1 2 3 4 5 6 7 8
| typedef long long ll; const int maxn = 67; ll res[maxn][maxn]; ll Comb(ll n, ll m){ if(m == 0|| n == m) return 1; if(res[n][m]!=0) return res[n][m]; return res[n][m] = C(n-1, m-1)+C(n-1, m); }
|
Lucas定理
p要求为素数,p<=1e5, n, m<=1e18
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
| int n, m, p; typedef long long ll; ll ex_gcd(ll a, ll b, ll &x, ll &y){ if(a == 0&&b == 0) return -1; if(b ==0){ x=1, y=0; return a; } ll d=ecx_gcd(b, a%b, y, x); y -= a/b*x; return d; } ll inv(ll a, ll n){ ll x, y; ll d = ex_gcd(a, n, x, y); if(d!=1) return -1; else return (x%n+n)%n; } int C(int n, int m){ int ans = 1; for(int i=1; i<=m; i++){ ans = ans*(n-m+i)%p; ans = ans*inv(i, p)%p; } return ans; } int lucas(int n, int m){ if(m == 0) return 1; return C(n%p, m%p)*lucas(n/p, m/p)%p; }
|
p不为质数的组合数求解
先将分子分母进行相应的质因子分解,然后消去分母,最后进行快速幂。
4C默写
搞完就删
堆排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77
| #include <bits/stdc++.h> using namespace std; const int maxn = 1e3+10; int heap[maxn]; int n; void downAdjust(int low, int high){ int i=low, j=2*i; while(j<=high){ if(j+1<=high&&heap[j+1]>heap[j]){ j++; } if(heap[j]>heap[i]){ swap(heap[i], heap[j]); i = j; j = i*2; } else break; } } void creat_heap(){ for(int i=n/2; i>=1; i--){ downAdjust(i, n); } } void deletetop(){ heap[1] = heap[n--]; downAdjust(1, n); } void upAdjust(int low, int high){ int i=high, j=i/2; while(j>=low){ if(heap[j]<heap[i]){ swap(heap[i], heap[j]); i = j; j = i/2; } else break; } } void insert_heap(int x){ heap[++n] = x; upAdjust(1, n); } void heapsort(){ creat_heap(); for(int i=n; i>=1; i--){ swap(heap[i], heap[1]); downAdjust(1, i-1); } } int main() { scanf("%d", &n); for(int i=1; i<=n; i++){ scanf("%d", &heap[i]); } creat_heap(); for(int i=1; i<=n; i++){ printf("%d ", heap[i]); } heapsort(); for(int i=1; i<=n; i++){ printf("%d ", heap[i]); } return 0; }
|
树的层序遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68
| #include <bits/stdc++.h> using namespace std; const int maxn = 1e3+10; struct Node{ int data; Node *lchild, *rchild; Node(){ this->data = -1; this->lchild = this->rchild = NULL; } }; int pre[maxn]; int in[maxn]; Node* build(int prel, int prer, int inl, int inr){ if(prel>prer) return NULL; Node *root = new Node; root->data = pre[prel]; int k; for(k=inl; k<=inr; k++){ if(pre[prel] == in[k]) break; } int num = k-inl; root->lchild = build(prel+1, prel+num, inl, k-1); root->rchild = build(prel+num+1, prer, k+1, inr); return root; } void post_order(Node *root){ if(root == NULL) return; post_order(root->lchild); post_order(root->rchild); printf("%d ", root->data); } void layer_order(Node *root){ queue<Node*> q; q.push(root); while(!q.empty()){ Node *temp = q.front(); q.pop(); printf("%d ", temp->data); if(temp->lchild != NULL) q.push(temp->lchild); if(temp->rchild != NULL) q.push(temp->rchild); } } int n; int main(){ scanf("%d", &n); for(int i=0; i<n; i++) scanf("%d", &pre[i]); for(int i=0; i<n; i++) scanf("%d", &in[i]); Node *root = build(0, n-1, 0, n-1); post_order(root); printf("\n"); layer_order(root); return 0; }
|
最长回文串
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
| #include <bits/stdc++.h> using namespace std; const int maxn = 1e3+10; string str; int dp[maxn][maxn]; int main() { getline(cin, str); memset(dp, 0, sizeof(dp)); int len = str.length(); int ans = 1; for(int i=0; i<len; i++){ dp[i][i] = 1; if(i+1<len){ if(str[i] == str[i+1]){ dp[i][i+1]=1; ans = 2; } } } for(int l=3; l<=len; l++){ for(int i=0; i+l-1<len; i++){ int j = i+l-1; if(str[i] == str[j] &&dp[i+1][j-1]){ dp[i][j] = 1; ans = l; } } } printf("%d\n", ans); }
|
scc
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90
| #include <iostream> #include <cstring> #include <cstdio> #include <vector> using namespace std; const int maxn = 1e3+10; vector<int> G[maxn]; vector<int> rG[maxn]; bool vis[maxn]; int index[maxn]; vector<int> vs; void add_edge(int u, int v){ G[u].push_back(v); rG[v].push_back(u); } int n, m; void dfs(int u){ vis[u] = true; for(int i=0; i<G[u].size(); i++){ if(!vis[G[u][i]]) dfs(G[u][i]); } vs.push_back(u); } void rdfs(int v, int k){ vis[v] = true; index[v] = k; for(int i=0; i<rG[v].size(); i++){ if(!vis[rG[v][i]])rdfs(rG[v][i], k); } } int scc(){ memset(vis, 0, sizeof(vis)); vs.clear(); for(int i=0; i<n; i++){ if(!vis[i]) dfs(i); } memset(vis, 0, sizeof(vis)); int k = 0; for(int i=vs.size()-1; i>=0; i--){ if(!vis[vs[i]]){ rdfs(vs[i], k++); } } printf("%d\n", k); return k; } int main() { while(~scanf("%d%d", &n, &m)){ for(int i=0; i<n; i++){ G[i].clear(); rG[i].clear(); } int u, v; for(int i=0; i<m; i++){ scanf("%d%d", &u, &v); add_edge(u-1, v-1); } scc(); for(int i=0; i<n; i++){ printf("%d: %d\n", i, index[i]); } } return 0; }
|
最长上升子序列
感觉运用了贪心的细想,不断的更新最长的子序列。
用二分查找的方法找到一个位置,使得\(num\gt b[i-1] 并且num\lt b[i],并用num代替b[i]\)
注意二分的总结
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
| #include <bits/stdc++.h> using namespace std; const int maxn = 1e5+10; int a[maxn], b[maxn]; int n; int len; int bi(int num){ int L=1, R=len; while(L<=R){ int M = (L+R)/2; if(num>=b[M]) L = M-1; else R = M-1; } printf("len: %d\n", L); return L; } int main() { while(~scanf("%d", &n)){ for(int i=1; i<=n; i++) scanf("%d", &a[i]); len=1; b[1] = a[1]; for(int i=2; i<=n; i++){ if(a[i]>=b[len]){ b[++len] = a[i]; } else{ int pos = bi(a[i]); b[pos] = a[i]; } } printf("%d\n", len); for(int i=1; i<=len; i++){ printf("%d ", b[i]); } printf("\n"); } return 0; }
|