有向图的最小生成树，用的算法是朱刘算法

有向图的最小生成树

定义

• 恰好有一个入度为0的节点，该节点被称为根节点
• 其他的节点入度为1
• 从根节点可以到达任意的节点

最重要的思想

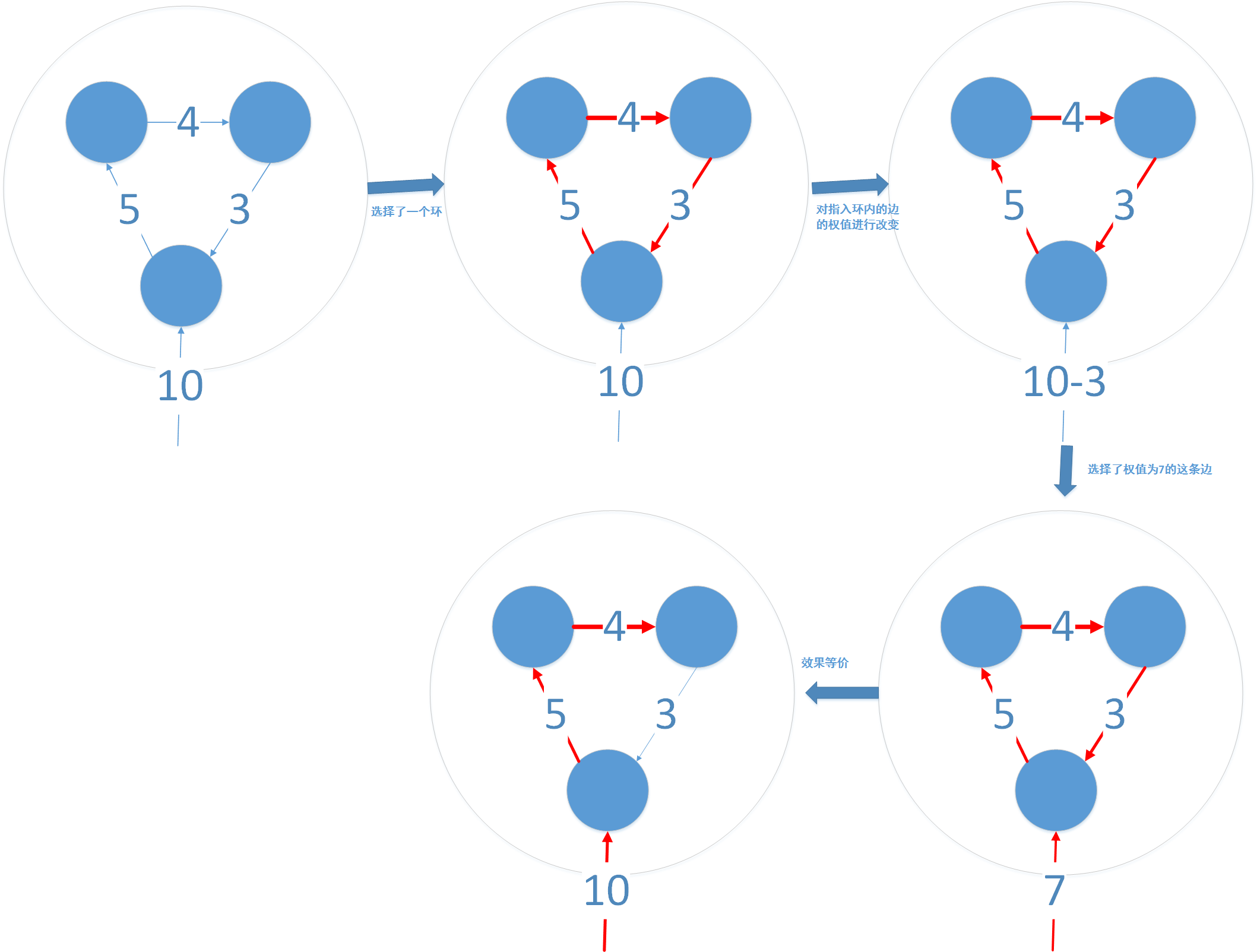
资料及代码的参考来源

最小树形图——朱刘算法(Edmonds)

代码

/*
最小树形图
朱刘算法模板
时间复杂度O(nm)
数据为int型
*/
#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 1010
#define MAXM 1000000+10
#define INF 0x3f3f3f3f
#include <iostream>
using namespace std;
struct Edge
{
    int from, to, cost;
};
Edge edge[MAXM];
int pre[MAXN];//存储父节点
int vis[MAXN];//标记作用
int id[MAXN];//id[i]记录节点i所在环的编号
int in[MAXN];//in[i]记录i入边中最小的权值
int N, M;//N个点 M条有向边
int zhuliu(int root, int n, int m, Edge *edge)//root根 n点数 m边数
{
    int res = 0, u, v;
    while(1)
    {
        for(int i = 0; i < n; i++)
            in[i] = INF;//初始化
        for(int i = 0; i < m; i++)
        {
            Edge E = edge[i];
            if(E.from != E.to && E.cost < in[E.to])
            {
                pre[E.to] = E.from;//记录前驱
                in[E.to] = E.cost;//更新
            }
        }
        for(int i = 0; i < n; i++)
            if(i != root && in[i] == INF)
                return -1;//有其他孤立点 则不存在最小树形图
        //找有向环
        int tn = 0;//记录当前查找中 环的总数
        memset(id, -1, sizeof(id));
        memset(vis, -1, sizeof(vis));
        in[root] = 0;//根
        for(int i = 0; i < n; i++)
        {
            res += in[i];//累加
            v = i;
            //找图中的有向环 三种情况会终止while循环
            //1,直到出现带有同样标记的点说明成环
            //2,节点已经属于其他环
            //3,遍历到根
            while(vis[v] != i && id[v] == -1 && v != root)
            {
                vis[v] = i;//标记
                v = pre[v];//一直向上找
            }
            //因为找到某节点属于其他环  或者 遍历到根  说明当前没有找到有向环
            if(v != root && id[v] == -1)//必须上述查找已经找到有向环
            {
                for(int u = pre[v]; u != v; u = pre[u])
                    id[u] = tn;//记录节点所属的 环编号
                id[v] = tn++;//记录节点所属的 环编号  环编号累加
            }
        }
        if(tn == 0) break;//不存在有向环
        //可能存在独立点
        //cout<<"test1"<<" "<<tn<<endl;
        for(int i = 0; i < n; i++)
            if(id[i] == -1){
                id[i] = tn++;//环数累加
                //cout<<i<<endl;
            }
        //cout<<"test2"<<tn<<endl;
        //对有向环缩点  和SCC缩点很像吧
        for(int i = 0; i < m; i++)
        {
            v = edge[i].to;
            edge[i].from = id[edge[i].from];
            edge[i].to = id[edge[i].to];
            //<u, v>有向边
            //两点不在同一个环 u到v的距离为 边权cost - in[v]
            if(edge[i].from != edge[i].to)
                edge[i].cost -= in[v];//更新边权值 继续下一条边的判定
        }
        n = tn;//以环总数为下次操作的点数 继续执行上述操作 直到没有环
        root = id[root];
//        for(int i=0; i<N; i++){
//            cout<<id[i]<<" ";
//        }
//        cout<<endl;
    }
    return res;
}

void getMap(){
    int u, v, w;
    for(int i=0; i<M; i++){
        scanf("%d%d%d", &u, &v, &w);
        edge[i] = Edge{u-1, v-1, w};
    }
}
int main()
{

    while(scanf("%d%d", &N, &M) != EOF)
    {
        getMap();//建图  注意去除自环  自己到自己的权值为无穷大
        int ans = zhuliu(0, N, M, edge);
        if(ans == -1)
            printf("-1\n");//不存在
        else
            printf("%d\n", ans);


    }
    return 0;
}
/*
7 15
1 2 9
4 1 3
1 5 5
2 3 3
3 2 7
2 4 9
5 4 4
6 5 3
4 3 8
4 6 5
3 6 9
3 7 6
7 3 4
6 7 4
7 6 8
*/

未解决的问题