中国剩余定理的应用,不涉及相应的公式的推导。
而又要分成两种情况:
- 模数相互互质(并不要求模数是质数,只要两两互质就行了)
- 模数不互质
模数两两互质的情况
之前一直害怕中国剩余定理的推导,知道我看到下面的大白话:
大白话讲解中国剩余定理

首先列出一个求解的过程,然后结合上面的讲解,说明求解的过程:
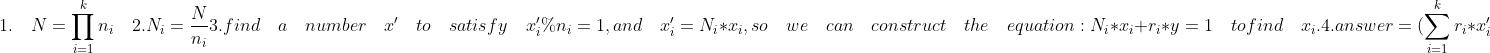\%N=(\sum_{i=1}^{k}r_i*N_i*x_i)\%N)
说明:
变量含义的说明:
\(r_i\):第i个式子的remainder, 也就是余数
\(n_i\):第i个式子的模数
1.第一步全部乘起来为后面做准备,不过数一课件中N为所有模数的最小公倍数,应该都可以吧除非有数的溢出。
2.单独求一个数的特殊的数,因此除掉那一个数。
3.求一个特殊的数字,这个数字模\(a_i\)为1
4.\((特殊的数字*r_i)\%n_i = r_i)\), 最后把它们都加起来就行了。
题目
fzoj1402
hdu1370
题意
题解
很裸的中国剩余定理的题目
AC代码
FZoj坑的要死,输出长整型必须是I64d,试了好几发
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41
| #include <iostream> #include <cstring> #include <cstdio> using namespace std; typedef long long ll; const int maxn = 15; ll n[maxn], r[maxn]; int num; ll ex_gcd(ll a, ll b, ll &x, ll &y){ if(a == 0&& b == 0) return -1; if(b == 0){ x = 1; y = 0; return a; } ll d = ex_gcd(b, a%b, y, x); y -= a/b*x; return d; } ll china_remainder(){ ll N = 1; for(int i=0; i<num; i++) N*=n[i]; ll ans = 0; for(int i=0; i<num; i++){ ll N_i = N/n[i]; ll x, y; ex_gcd(N_i, n[i], x, y); x = (x%n[i]+n[i])%n[i]; ans = (ans+r[i]*x*N_i%N)%N; } printf("%I64d\n", ans); return ans; } int main(){ while(~scanf("%d", &num)){ for(int i=0; i<num; i++) scanf("%I64d%I64d", &n[i], &r[i]); china_remainder(); } return 0; }
|
模数不互质的中国剩余定理
推导的过程好复杂,采用了合并的思想
模数不互质的情况说明

题目
poj 2891
AC 代码
直接超别人的代码了,积累一下,知道有这么个东西
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91
| #include <iostream> #include <cstdio> #include <cstring> using namespace std; typedef __int64 int64; int64 Mod; int64 gcd(int64 a, int64 b) { if(b==0) return a; return gcd(b,a%b); } int64 Extend_Euclid(int64 a, int64 b, int64&x, int64& y) { if(b==0) { x=1,y=0; return a; } int64 d = Extend_Euclid(b,a%b,x,y); int64 t = x; x = y; y = t - a/b*y; return d; } int64 inv(int64 a, int64 n) { int64 x,y; int64 t = Extend_Euclid(a,n,x,y); if(t != 1) return -1; return (x%n+n)%n; } bool merge(int64 a1, int64 n1, int64 a2, int64 n2, int64& a3, int64& n3) { int64 d = gcd(n1,n2); int64 c = a2-a1; if(c%d) return false; c = (c%n2+n2)%n2; c /= d; n1 /= d; n2 /= d; c *= inv(n1,n2); c %= n2; c *= n1*d; c += a1; n3 = n1*n2*d; a3 = (c%n3+n3)%n3; return true; } int64 China_Reminder2(int len, int64* a, int64* n) { int64 a1=a[0],n1=n[0]; int64 a2,n2; for(int i = 1; i < len; i++) { int64 aa,nn; a2 = a[i],n2=n[i]; if(!merge(a1,n1,a2,n2,aa,nn)) return -1; a1 = aa; n1 = nn; } Mod = n1; return (a1%n1+n1)%n1; } int64 a[1000],b[1000]; int main() { int i; int k; while(scanf("%d",&k)!=EOF) { for(i = 0; i < k; i++) scanf("%I64d %I64d",&a[i],&b[i]); printf("%I64d\n",China_Reminder2(k,b,a)); } return 0; }
|
未解决的问题

