polya定理的应用

ACM

前两天本来是开了单独的一个组合数学的博文，但是发现里面的知识点基本都会了，特地把这个定理拿出来讲解。
感觉最近一直在学习新的算法，过得很充实，但是总是隐隐感觉不太对劲，没有形成自己的思维。后两周的比赛加油啊。

一道题目

有一个2*2的方阵，用黑白两种颜色进行染色，通过旋转重合的方案算是同一种方案，问有多少种不同的方案。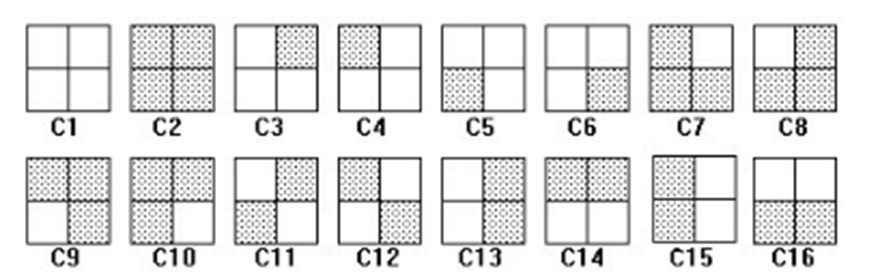

这道题目的答案是6，怎么样解决这个问题呢？

Burnside引理

{g1, g2, g3, g4} = {旋转0°， 逆时针旋转90°，逆时针旋转180°, 逆时针旋转270° };

注释：集合中任意种变化的组合必须包含在集合中，即必须要具有封闭性。

Burnside引理具体要计算每一种变换的不动点的数目，时间复杂度是指数级别的。
因此，就引入了Polya定理（然而并不会证明）

Polya定理

  • G是{1,2,…,n}的一个置换群
  • 用m种颜色给1~n进行染色，不同染色方案数为

首先对每一个格子进行相应的编号，称之为标准态：


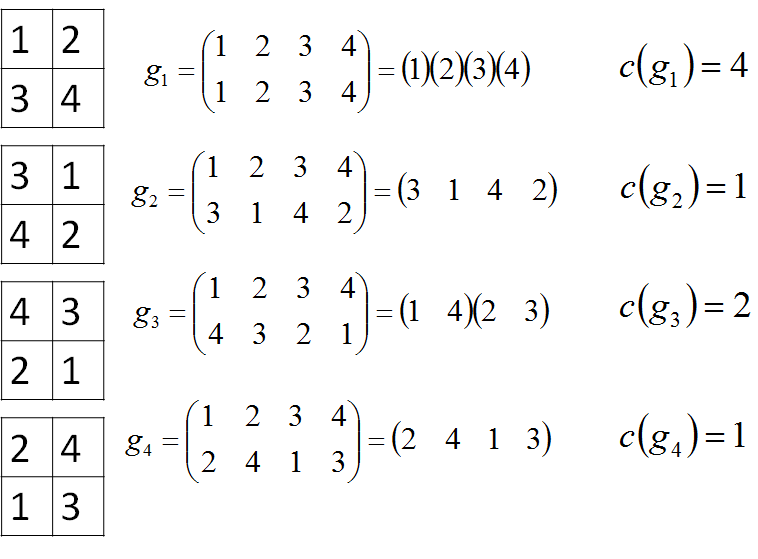
其中，c(g)表示在g这种姿态下的循环节的个数。

Qusetion:Polya能替代Burnside定理吗？

珠子的染色问题

题目

poj 2409

题意

  • 给定一个珠子的颜色数目为c， 珠子的个数为s。其中翻转、旋转后与之前的情形有重复的情况的条件下，算一种染色方案。
  • 问一共有多少种不同的染色方案

题解

Polya定理的应用：
分两种情况：

旋转：

一个有n种旋转方式：{转动0个珠子， 转动1个珠子, …, 转动i个珠子，…, 转动n-1个珠子}。
其中\(\frac{n}{gcd(n, i)}\)个珠子构成一个循环节，那么一共有gcd(n, i)个循环节。

翻转：

有两种情况：

当n为奇数的时候：

有n条翻转的对称轴，两个珠子为一组，构成\(\frac{n-1}{2}\)个循环节，剩下的一个珠子单独构成一个循环节。

当n为偶数的时候：

当一条对称轴穿过两个珠子的情况：
共有\(\frac{n}{2}\)条对称轴，两个珠子为一组，构成\(\frac{n-2}{2}\)个循环节，剩下在对称轴上面的两个珠子构成两个循环节。一共构成个循环节。

当对称轴不穿过任何的珠子的时候，以对称轴为中心，两个为一组，构成\(\frac{n}{2}\)个循环节。

变换的种类的个数

旋转有n种变换，翻转的时候，不论奇偶，都有n种变换。总共有2n种变换

总的式子

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <algorithm>
using namespace std;
int main()
{
    int c, s;
    while(cin>>c>>s){
        if(c+s == 0) break;
        if(s%2){
            int ans = 0;
            for(int i=0; i<s; i++){
                int mul = 1;
                for(int j=0; j<__gcd(s, i); j++){
                    mul*=c;
                }
                ans+=mul;
            }
            int mul = 1;
            for(int i=0; i<(s-1)/2+1; i++){
                mul*=c;
            }
            ans += s*mul;
            cout<<ans/(2*s)<<endl;
        }
        else{
            int ans = 0;
            for(int i=0; i<s; i++){
                int mul = 1;
                for(int j=0; j<__gcd(s, i); j++){
                    mul*=c;
                }
                ans+=mul;
            }
            int mul = 1;
            for(int i=0; i<s/2; i++){
                mul*=c;
            }
            ans += s/2*mul;
            mul = 1;
            for(int i=0; i<(s-2)/2+2; i++){
                mul*=c;
            }
            ans += s/2*mul;
            cout<<ans/(2*s)<<endl;
        }
    }
    return 0;
}

因为这道题目规模比较的小，还可以直接写出这些置换，用Burnside.

未解决的问题

Polya能代替Burnside吗

本文标题:polya定理的应用

文章作者:Babydragon

发布时间:2018-03-22, 18:27:26

最后更新:2018-03-23, 13:29:06

原始链接:http://baolintian.github.io/2018/03/22/polya定理的应用/

许可协议: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

文章目录
  1. 1. 一道题目
    1. 1.1. Burnside引理
    2. 1.2. Polya定理
  2. 2. Qusetion:Polya能替代Burnside定理吗？
  3. 3. 珠子的染色问题
    1. 3.1. 题目
    2. 3.2. 题意
    3. 3.3. 题解
      1. 3.3.0.1. 旋转：
      2. 3.3.0.2. 翻转：
        1. 3.3.0.2.1. 当n为奇数的时候：
        2. 3.3.0.2.2. 当n为偶数的时候：
      3. 3.3.0.3. 变换的种类的个数
    4. 3.3.1. 总的式子
  4. 3.4. AC代码
  • 4. 未解决的问题
    • {{ live2d() }}