2018-04-18

cf-round754 div2

cf中的一个数学题

C

一开始我知道我写完肯定会T，但是还是写了下去，然而WA7，我想怎么会不是T呢，T了才有改进的动力啊。
第二天的中午才发现了问题，原来由于数的乘积非常的大，因此仅仅一次的取正是不行的。
num = (num+mod)%mod;变成了num = (num+mod*n)%mod;

然后当然就理所当然的T了。

对等式进行相应的化简
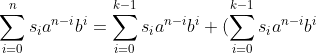$\sum_{i=0}^{n}s_ia^{n-i}b^i = \sum_{i=0}^{k-1}s_ia^{n-i}b^i+(\sum_{i=0}^{k-1}s_ia^{n-i}b^i)·(a^{-k}b^k)+\dots+(\sum_{i=0}^{k-1}s_ia^{n-i}b^i)(a^{-k\frac{n+1}{k}-1}b^{k\frac{n+1}{k}-1})\\ = \sum_{i=0}^{k-1}s_ia^{n-i}b^i(1+a^{-k}b^k+a^{-2k}b^{2k}+\dots + a^{-k\frac{n+1}{k}-1}b^{k\frac{n+1}{k}-1})\\ = \sum_{i=0}^{k-1}s_ia^{n-i}b^i*(\frac{1-(a^{-k}b^k)^{\frac{n+1}{k}}}{1-(a^{-k}b^k)})$

前面一部分用快速幂，因为1e9+9是质数，任意数对该数的逆元必定存在。后面的部分用逆元来搞就行了

AC代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9+9;
ll pow_mod(ll a, ll b){
    ll ans = 1ll;
    while(b){
        if(b&1){
            ans=(ans*a)%mod;
        }
        a = a*a%mod;
        b>>=1;
    }
    return ans;
}
void extgcd(ll a,ll b,ll& d,ll& x,ll& y){
    if(!b){ d=a; x=1; y=0;}
    else{ extgcd(b,a%b,d,y,x); y-=x*(a/b); }
}
ll inverse(ll a,ll n){
    ll d,x,y;
    extgcd(a,n,d,x,y);
    return d==1?(x+n)%n:-1;
}
ll n ,a, b, k;
string op;
int main()
{
    ios::sync_with_stdio(false);
    while(cin>>n>>a>>b>>k){
        cin>>op;
        ll ans = 0;
        for(int i=0; i<k; i++){
            ll num = 0;
            char temp = op[i];
            if(temp == '-'){
                num = (-1ll)*pow_mod(a, n-i)*pow_mod(b, i)%mod;
                num = (num+mod*n)%mod;
            }
            else{
                num = pow_mod(a, n-i)*pow_mod(b, i)%mod;
                num = (num+mod*n)%mod;
            }
            ans = (ans+num+mod)%mod;
        }
        //cout<<ans<<endl;
        ll q = (pow_mod(a, (mod-2)*k)*pow_mod(b, k))%mod;
        if(q == 1){
            cout<<ans*(n+1)/k%mod<<endl;
        }
        else{
            ll inverse_deno = inverse((q-1), mod);
            cout<<((ans*(pow_mod(q, (n+1)/k)-1ll)%mod)*inverse_deno%mod+n*mod)%mod<<endl;
        }
    }
    return 0;
}

D

一个思考题，第一眼看上去感觉在删边的时候要不断的维护删除的信息，感觉不可做。
但是看了别人的题解之后，发现删除的时候并不不需要维护。从底向上不断的删除就行了

题解

首先。若节点是偶数个，那么肯定不存在解，因为总共有奇数条边，每次删除偶数条边，最后不可能删完的。

d[i]: 表示的是i及i的子树中节点的总个数。
我们都是从d[i]为奇数的节点开始删除的，d[i]为奇数表示这个子树有偶数条边。因为从下往上删除，一定是符合要求的。
感觉这种不需要维护删除信息的思想非常的重要，把原来复杂的问题简单化。

还有，关同步大法好！！！！

AC代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5+10;
vector<int> num[maxn];
int d[maxn];
int n;
void dfs(int u, int fa){
    d[u] = 1;
    for(int i=0; i<num[u].size(); i++){
        if(num[u][i] == fa) continue;
        else{
            dfs(num[u][i], u);
            d[u] += d[num[u][i]];
        }
    }
}
void solve(int u, int fa){
    for(int i=0; i<num[u].size(); i++){
        int v = num[u][i];
        if(v == fa) continue;
        else{
            if(d[v]%2==0){
                solve(v, u);
            }
        }
    }
    cout<<u<<endl;
    for(int i=0; i<num[u].size(); i++){
        int v = num[u][i];
        if(v == fa) continue;
        else{
            if(d[v]%2==1){
                solve(v, u);
            }
        }
    }
}
int main(){
    ios::sync_with_stdio(false);
    while(cin>>n){
        int rt;
        if(n%2==0){
            int temp;
            for(int i=0; i<n; i++) cin>>temp;
            cout<<"NO"<<endl;
        }
        else{
            cout<<"YES"<<endl;
            for(int i=1; i<=n; i++){
                int temp;
                cin>>temp;
                if(temp == 0) rt = i;
                num[temp].push_back(i);
            }
            dfs(rt, -1);
            solve(rt, -1);
        }
    }
    return 0;
}

未解决的问题

本文标题:cf-round754 div2

文章作者:Babydragon

发布时间:2018-04-18, 13:10:54

最后更新:2018-04-19, 20:49:50

原始链接:http://baolintian.github.io/2018/04/18/cf-round754-div2/

许可协议: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。