#ifndef NOSTDCPP
#include <bits/stdc++.h>
#else
#include <algorithm>
#include <bitset>
#include <cassert>
#include <climits>
#include <complex>
#include <cstring>
#include <cstdio>
#include <deque>
#include <exception>
#include <functional>
#include <iomanip>
#include <iostream>
#include <istream>
#include <iterator>
#include <list>
#include <map>
#include <ostream>
#include <queue>
#include <set>
#include <sstream>
#include <stack>
#include <string>
#include <typeinfo>
#include <utility>
#include <valarray>
#include <vector>
#endif
# ifdef Linux_System
# define getchar getchar_unlocked
# define putchar putchar_unlocked
# endif
# define RESET(_) memset(_, 0, sizeof(_))
# define RESET_(_, val) memset(_, val, sizeof(_))
# define fi first
# define se second
# define pb push_back
# define midf(x, y) ((x + y) >> 1)
# define DXA(_) ((_ << 1))
# define DXB(_) ((_ << 1) | 1)
# define begin __Chtholly__
# define x1 __Mercury__
# define y1 __bbtl04__
# define index __ikooo__
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef vector <int> vi;
typedef set <int> si;
typedef pair <int, int> pii;
typedef long double ld;
const int MOD = 1e9 + 7;
const int maxn = 300009;
const int maxm = 300009;
const ll inf = 1e18;
const double pi = acos(-1.0);
const double eps = 1e-6;
ll myrand(ll mod){return ((ll)rand() << 32 ^ (ll)rand() << 16 ^ rand()) % mod;}
template <class T>
inline bool scan_d(T & ret)
{
char c;
int sgn;
if(c = getchar(), c == EOF)return false;
while(c != '-' && (c < '0' || c > '9'))c = getchar();
sgn = (c == '-') ? -1 : 1;
ret = (c == '-') ? 0 : (c - '0');
while(c = getchar(), c >= '0' && c <= '9')
ret = ret * 10 + (c - '0');
ret *= sgn;
return true;
}
#ifdef Cpp11
template <class T, class ... Args>
inline bool scan_d(T & ret, Args & ... args)
{
scan_d(ret);
scan_d(args...);
}
#define cin.tie(0); cin.tie(nullptr);
#define cout.tie(0); cout.tie(nullptr);
#endif
inline bool scan_ch(char &ch)
{
if(ch = getchar(), ch == EOF)return false;
while(ch == ' ' || ch == '\n')ch = getchar();
return true;
}
template <class T>
inline void out_number(T x)
{
if(x < 0)
{
putchar('-');
out_number(- x);
return ;
}
if(x > 9)out_number(x / 10);
putchar(x % 10 + '0');
}
int nn, d, k;
ll m;
struct matrix
{
double a[1009][1009];
int n;
void clear(){RESET(a), n = 0;}
};
matrix tmp, tmp2, f, ee, q1, q2;
void one(int n)
{
tmp.clear();
tmp.n = n;
for(int i = 1; i <= n; ++ i) tmp.a[i][i] = 1;
}
void mul(const matrix &ma, const matrix &b)
{
tmp.clear();
tmp.n = ma.n;
for(int i = 1; i <= ma.n; ++ i)
for(int j = 1; j <= ma.n; ++ j)
tmp.a[1][j] = (tmp.a[1][j] + ma.a[1][i] * b.a[i][j]);
for(int i = 2; i <= ma.n; ++ i)
for(int j = 1; j <= ma.n; ++ j)
tmp.a[i][j] = tmp.a[i - 1][j == 1 ? ma.n : j - 1];
}
void pow(matrix &q, int b)
{
q1.n = q.n;
one(q.n);
q2 = tmp;
for(int i = 1; i <= tmp.n; ++ i)
for(int j = 1; j <= tmp.n; ++ j)
q1.a[i][j] = q.a[i][j];
while(b)
{
if(b & 1)
{
mul(q1, q2);
q2 = tmp;
}
b >>= 1;
mul(q1, q1);
q1 = tmp;
}
}
double beg[1000], now[1000];
int main()
{
scanf("%d %d %d", &nn, &m, &k);
for(int i = 1; i <= nn; ++ i) scanf("%lf", beg + i);
f.clear();
f.n = nn;
for(int i = 1; i <= nn; ++ i)
{
f.a[i][i] = -1.0 / (double)m + 1.0;
f.a[i][i == nn ? 1 : i + 1] = 1.0 / (double)m;
}
pow(f, k);
ee = q2;
for(int i = 1; i <= nn; ++ i)
for(int j = 1; j <= nn; ++ j)
{
now[i] = (now[i] + beg[j] * ee.a[j][i]);
}
for(int i = 1; i <= nn; ++ i) printf("%.3f\n", now[i]);
return 0;
}
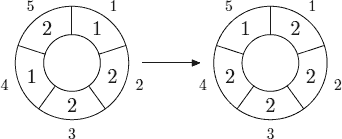
(这里故意不把 $m$ 带入矩阵)